研究紹介

ホーム > 研究

概要

研究者プロフィール
主な研究内容
その他

相対論的磁気リコネクションの運動論研究

プラズマ中で逆向きの磁力線が向かいあう電流シート構造は、宇宙空間のプラズマ現象を議論するための基本構造のひとつです。電流シート内では、磁力線が繋ぎ変わって磁場エネルギーをプラズマエネルギーに解放する「磁気リコネクション」が起きることが知られていて、太陽フレアや磁気圏サブストームとの関連で詳細な研究が行われてきました。高エネルギー天体分野では、パルサーからローレンツ因子γ～106 もの高速で吹き出す電子・陽電子流（パルサー風）の内部に電流シート構造が存在して、磁気エネルギーの散逸に関わっているという説が有力視されています（Coroniti et al. 1990 ApJ）。また、ガンマ線バーストについても、強磁場環境でのリコネクションを中心とした磁気散逸が活発に議論されています（Zhang & Yan 2011 ApJ, McKinney & Uzdensky 2011 MNRAS）。しかし、このような相対論プラズマ環境での磁気リコネクション・電流シート構造の性質は、ほとんど研究されていませんでした。

我々は、主にプラズマ粒子（Particle-In-Cell; PIC）シミュレーションを用いて、電子・陽電子プラズマ中の相対論的磁気リコネクション及び電流シートの基礎研究を行いました。PIC 法は、多数の仮想プラズマ粒子の運動を電磁場中の運動方程式を用いて解き、得られた電流・電荷分布を用いて電磁場を発展させることで、プラズマ系の時間発展を自己無憧着的に解き進める方法です。大きな計算機能力を必要とする反面、詳細なプラズマ物理を扱うことができる利点があります。

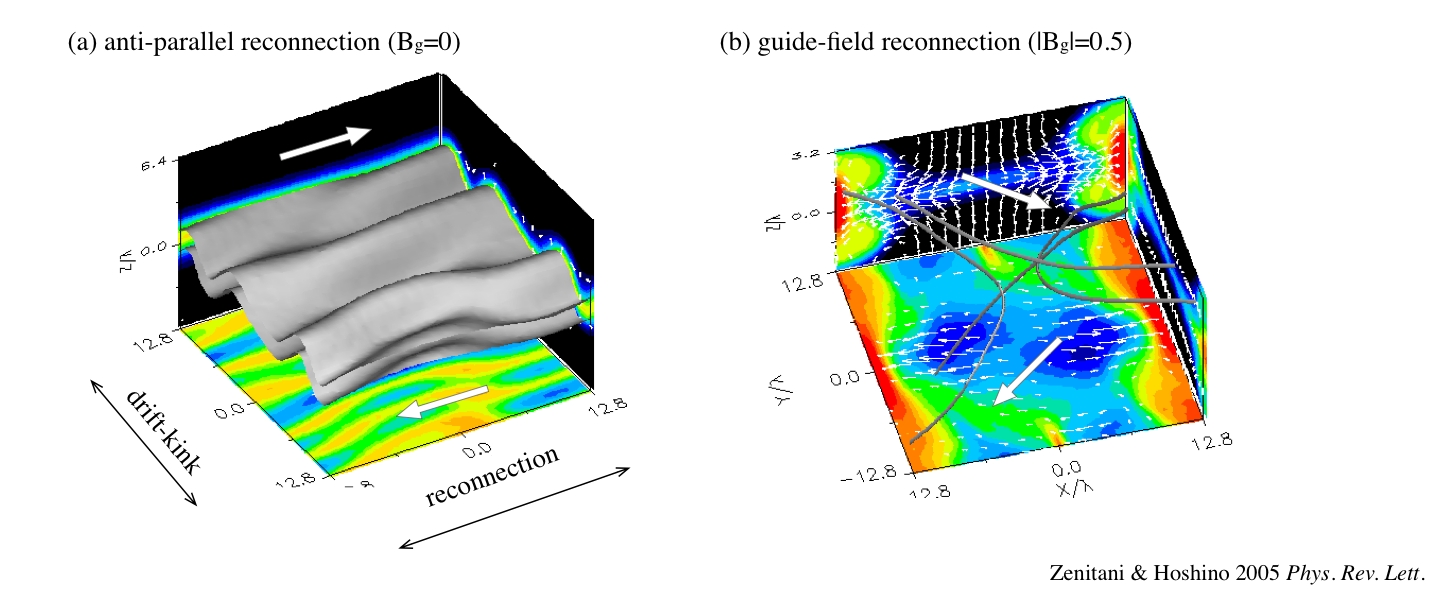
まず、反平行磁場を含む２次元平面で PIC シミュレーションを行い、磁力線が繋ぎ変わる領域から吹き出すジェット（アウトフロー）が光速近くに達する相対論的磁気リコネクションを再現することに世界で初めて成功しました。そして、磁力線が繋ぎ変わる領域の近くで、リコネクション電場によって強い粒子加速が起きていることを発見しました [1,4]。一方、リコネクションとは垂直の２次元面では、相対論ドリフトキンク不安定というフルート不安定が成長して乱流的に崩壊し、プラズマを熱化します [2,4]。３次元ではドリフトキンク不安定が速く成長しますが（図a）、背景磁場が捩じれている（ガイド磁場成分を持つ）場合には、ガイド磁場がドリフトキンク不安定を安定化するため、リコネクションと粒子加速が起きます（図b）[3,5]。磁場トポロジーの違いによって電流シート中の物理過程が切り替わり、磁気エネルギーの解放先がプラズマの熱的成分から非熱的成分に変わってしまうわけです [3]。これはまさに、宇宙空間中のエネルギー配分にプラズマ物理の理解が欠かせないことを象徴しています。さらに、リコネクションジェットが周辺プラズマと衝突する領域で、相対論的ワイベル不安定が磁場を生成することもわかりました [6]。ワイベル不安定（Weibel 1959 PRL）は、プラズマ分布関数の非等方のエネルギーから乱流磁場を生成する不安定で、相対論衝撃波での衝撃波統計加速の散乱体として注目されていましたが、磁気リコネクション系でも重要な役割を果たすことが実証されたわけです。総括すると、相対論リコネクション・電流シート系で起きる主要なプラズマ素過程を発見し尽くし、それぞれの役割を議論したことになります。

2011年に「かに星雲」でガンマ線フレアが発見され、その起源として磁気リコネクションが有力視されて以来、世界各地で相対論リコネクションの運動論研究が行われています。我々の一連の研究成果は、これらの後継研究の出発点になっています。

3D relativistic reconnection

査読論文
  1. S. Zenitani and M. Hoshino, The Generation of Nonthermal Particles in Relativistic Magnetic Reconnection of Pair Plasmas, Astrophys. J. Lett. 562, L63-L66 (2001)
  2. S. Zenitani and M. Hoshino, Relativistic Particle Acceleration in a Folded Current Sheet, Astrophys. J. Lett. 618, L111-L114 (2005)
  3. S. Zenitani and M. Hoshino, Three-Dimensional Evolution of a Relativistic Current Sheet: Triggering of Magnetic Reconnection by the Guide Field, Phys. Rev. Lett. 95, 095001 (2005)
  4. S. Zenitani and M. Hoshino, Particle Acceleration and Magnetic Dissipation in Relativistic Current Sheet of Pair Plasmas, Astrophys. J. 670, 702-726 (2007)
  5. S. Zenitani and M. Hoshino, The Role of the Guide Field in Relativistic Pair Plasma Reconnection, Astrophys. J. 677, 530-544 (2008)
  6. S. Zenitani and M. Hesse, The role of the Weibel instability at the reconnection jet front in relativistic pair plasma reconnection, Phys. Plasmas 15, 022101 (2008)
  7. S. Zenitani and M. Hesse, Self-regulation of the Reconnecting Current Layer in Relativistic Pair Plasma Reconnection, Astrophys. J. 684, 1477-1485 (2008)
  8. S. Zenitani, Dissipation in relativistic pair-plasma reconnection: revisited, Plasma Physics and Controlled Fusion 60, 014028 (2018)
  9. M. Hesse and S. Zenitani, Dissipation in relativistic pair-plasma reconnection, Phys. Plasmas 14, 112102 (2007)
  10. S. Totorica, S. Zenitani, M. Machida, S. Matsukiyo, K. Sekiguchi, and A. Bhattacharjee, Exact Calculation of Nonideal Fields Demonstrates Dominance of Injection in Relativistic Reconnection, Astrophys. J. Lett. 752, L1 (2023)
  11. F. Guo, Y.-H. Liu, S. Zenitani, and M. Hoshino, Magnetic Reconnection and Associated Particle Acceleration in High-energy Astrophysics, Space Science Reviews 220, 43 (2024)
解説記事
  1. 銭谷誠司, 高橋博之, 新たなリコネクション研究の芽: 相対論領域のリコネクション, プラズマ・核融合学会誌 89, 845-847 (2013)
その他資料


[もどる]

相対論的磁気リコネクションの流体論研究

大規模のプラズマ現象を扱うためには磁気流体（MHD）近似が有効です。相対論プラズマ分野でも 1990 年代から相対論的磁気流体（RMHD）シミュレーションが行われるようになってきました。ところで、リコネクションのような磁気散逸問題を扱うためには電気抵抗を組み込んだ抵抗 MHD モデルが必要ですが、相対論的抵抗磁気流体（RRMHD）モデルについての基礎研究はほとんどありませんでした（Watanabe & Yokoyama 2006 ApJ, Komissarov 2007 MNRAS）。我々は、電子・陽電子を別々の流体として扱う相対論的２流体コードを開発して、相対論的磁気リコネクションの大規模発展を多流体シミュレーションで初めて再現しました [1]。そして続編論文では、方程式系を改良してエネルギー収支やガイド磁場効果などを議論しました [2]。さらに後続の RRMHD シミュレーションでは、リコネクションジェットが相対論的 Alfven 速度に達することや磁気島（プラズモイド）周辺に新しい衝撃波構造を作ることを報告しました [3]。これら一連の研究を通じて、相対論リコネクションの流体スケールでの性質がひととおり明らかになったわけです [6]。RRMHD シミュレーションを利用した共同研究では、「かに星雲」のガンマ線フレアの駆動メカニズム候補の１つとして、パルサー風中で電流層どうしが干渉して起きるダブル＝テアリングモード型リコネクションを提案しています [4,5]。

後で述べますが、このうち RRMHD 衝撃波研究は、非相対論のMHDリコネクション研究にも新しい展開をもたらしました。リコネクションの典型速度が音速を超えると、衝撃波などの超音速・遷音速特有の現象が表れます。その後、これらの現象をプラズマ物理と高速流体力学との関わりという視点で理解する研究が進んでいます。

高エネルギー天文学で広く使われている RMHD モデルは、相対論で簡単に破れるはずの電荷中性条件を強制しています。この不自然な仮定による副作用はよくわかっていません。相対論的多流体モデル [1,2] は最初から荷電分離に対応していますから、少なくとも一部の研究領域で RMHD モデルを置き換える可能性を秘めています。こうした背景もあって、相対論的多流体（２流体）モデルのコード開発・シミュレーション研究も進められています（Amano & Kirk 2013 ApJ, Barkov et al. 2014 MNRAS, Balsara et al. 2016 JCP）。

relativistic fluid reconnection

査読論文
  1. S. Zenitani, M. Hesse, and A. Klimas, Two-fluid Magnetohydrodynamic Simulations of Relativistic Magnetic Reconnection, Astrophys. J. 696, 1385-1401 (2009)
  2. S. Zenitani, M. Hesse, and A. Klimas, Relativistic Two-fluid Simulations of Guide Field Magnetic Reconnection, Astrophys. J. 705, 907-913 (2009)
  3. S. Zenitani, M. Hesse, and A. Klimas, Resistive Magnetohydrodynamic Simulations of Relativistic Magnetic Reconnection, Astrophys. J. Lett. 716, L214-L218 (2010)
  4. H. Baty, J. Pétri, and S. Zenitani, Explosive reconnection of double tearing modes in relativistic plasmas: application to the Crab flares, MNRAS Letters 436, L20 (2013)
  5. J. Pétri, M. Takamoto, H. Baty, and S. Zenitani, Explosive reconnection of double tearing modes in relativistic plasmas with application to the Crab nebula, Plasma Physics and Controlled Fusion 57, 014034 (2015)
  6. F. Guo, Y.-H. Liu, S. Zenitani, and M. Hoshino, Magnetic Reconnection and Associated Particle Acceleration in High-energy Astrophysics, Space Science Reviews 220, 43 (2024)
紀要（査読付）・解説記事
  1. S. Zenitani, M. Hesse, and A. Klimas, Fluid and Magnetofluid Modeling of Relativistic Magnetic Reconnection, AIP Conf. 1366, 138 (2011)
  2. 銭谷誠司, 高橋博之, 新たなリコネクション研究の芽: 相対論領域のリコネクション, プラズマ・核融合学会誌 89, 845-847 (2013)
解説記事・講演資料


[もどる]

無衝突磁気リコネクションの基礎研究

磁気リコネクションの性質は、磁力線が繋ぎかわる中心領域（Ｘ型の磁気中性線付近の狭い領域）の物理に左右されます。この中心領域は「磁気散逸領域」あるいは「磁気拡散領域」と呼ばれています。しかし、地球近傍の宇宙空間で起きる無衝突運動論プラズマでは、磁気拡散領域付近の構造は複雑で、その解釈・役割について意見がまとまっていません。例えば2000年前後には、プラズマの理想条件が成立しない（E + v×B ≠ 0）ことを手がかりにして拡散領域の構造を議論できると考えられていました。しかし実際は、運動論プラズマは様々な場所で理想条件を破るため、こうした議論が成り立たないことがわかってきたのです。この中心領域問題についての論争は今も続いています。

我々はこの重要問題に、次の３つのアプローチで挑んでいます。１つめは、磁気流体の基礎概念に立ち返ることです。我々は、真の「磁気散逸領域」を理解するためには、磁気エネルギーの散逸という観点から議論すべきだと考えました。そして、系に依存しない、ローレンツ不変なエネルギー散逸量（電子系散逸量 De）を導出し [1]、この量を使って磁気散逸領域を検出できることを PIC シミュレーションで示しました [1,2]。さらに「磁気拡散」の本来の意味を考えると、プラズマ理想条件の破れ（E + v×B ≠ 0）は拡散の必要条件に過ぎず、「拡散領域」と「散逸領域」も個別に定義できるはずです [5]。こうした議論はプラズマ物理の全域に適用できるため、例えば前者の電子系散逸量は、宇宙空間の運動論プラズマ乱流分野でも使われるようになってきました（Wan et al. 2012, 2015 PRL, Matthaeus et al. 2015 Phil. Trans. A）。

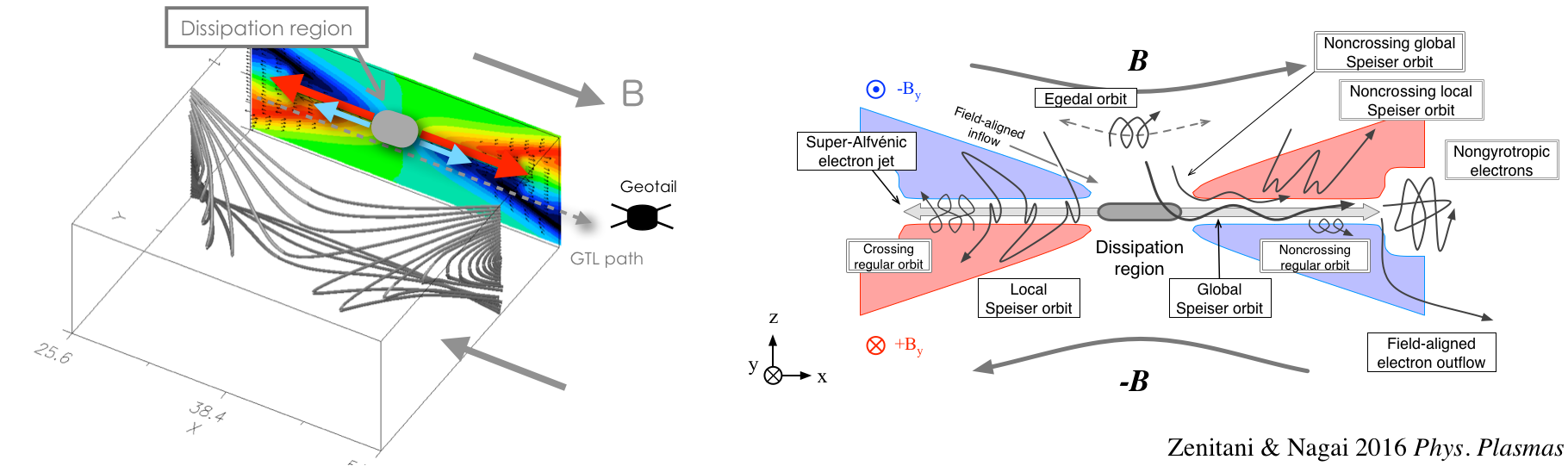
２つめのアプローチは、個々の粒子運動を見ることです。上記の議論が難しかった理由の１つは、運動論プラズマの振る舞いを、無理やり流体の枠組みで理解しようとしたからです。我々は、PIC シミュレーションでリコネクション系の粒子運動を丁寧に解析し、プラズマ理想条件が破れる領域（E + v×B ≠ 0）では、粒子は非ジャイロ回転タイプの軌道を通っていることを突き止めました [4,6,7]。議論の前提となるジャイロ回転（と E×B ドリフト運動）が成立しないため、そもそも理想条件を期待できなかったわけです。さらに詳しく調べると、大多数の電子がこれまで知られていなかった新しいタイプの軌道を通っていることがわかりました（図右 [6]）。これは、1980年代に完成したと思われていた粒子軌道論と、それを前提に構築された理論モデルの多くに再考を促す結果で、全米物理学連合のニュースリリースでも取り上げられています。この結果を起点に、今後、運動論リコネクションの物理を考え直していく必要があるでしょう。

３つめのアプローチは、理論・仮説を自然界で実証することです。我々は、上記の理論予想をジオテイル衛星の宇宙空間プラズマ観測に応用し、地球磁気圏夜側のリコネクション領域の中央付近で実際に磁気散逸が起きていたことを確認しました [3]。これは惑星磁気圏で磁気リコネクションの磁気散逸領域を直接検出した初めての研究で、ジオテイル衛星の主要観測成果の１つにも挙げられています。さらに衛星観測研究グループや核融合科学研究グループとの共同研究を進め、地球磁気圏夜側の磁気リコネクションの空間構造や、イオンの運動論物理の観測的証拠を議論しました [15-24]。これら一連の磁気リコネクション物理の問題を解明するために、2015年3月には NASA/Magnetospheric Multiscale (MMS) 衛星群 が打ち上げられ、地球近傍の宇宙空間で詳細なプラズマ観測を行なっています。我々の手法は、MMS 衛星のリコネクション領域の観測 (Burch et al. 2016 Science, Phan et al. 2018 Nature, Torbert et al. 2018 Science) で利用されています。

Fully kinetic reconnection

査読論文
  1. S. Zenitani, M. Hesse, A. Klimas, and M. Kuznetsova, New Measure of the Dissipation Region in Collisionless Magnetic Reconnection, Phys. Rev. Lett. 106, 195003 (2011)
  2. S. Zenitani, M. Hesse, A. Klimas, C. Black, and M. Kuznetsova, The inner structure of collisionless magnetic reconnection: The electron-frame dissipation measure and Hall fields, Phys. Plasmas 18, 122108 (2011); ibid. 21, 129906 (2014)
  3. S. Zenitani, I. Shinohara, and T. Nagai, Evidence for the dissipation region in magnetotail reconnection, Geophys. Res. Lett. 39, L11102 (2012)
  4. S. Zenitani, I. Shinohara, T. Nagai, and T. Wada, Kinetic aspects of the ion current layer in a reconnection outflow exhaust, Phys. Plasmas 20, 092120 (2013)
  5. S. Zenitani and T. Umeda, Some remarks on the diffusion regions in magnetic reconnection, Phys. Plasmas 21, 034503 (2014)
  6. S. Zenitani and T. Nagai, Particle dynamics in the electron current layer in collisionless magnetic reconnection, Physics of Plasmas 23, 102102 (2016)
  7. S. Zenitani, H. Hasegawa, and T. Nagai, Electron dynamics surrounding the X line in asymmetric magnetic reconnection, J. Geophys. Res. 122, 7396 (2017)
  8. A. Klimas, M. Hesse, and S. Zenitani, Particle-in-cell simulation of collisionless reconnection with open outflow boundaries, Phys. Plasmas 15, 082102 (2008)
  9. M. Hesse, S. Zenitani, and A. Klimas, The structure of the electron outflow jet in collisionless magnetic reconnection, Phys. Plasmas 15, 112102 (2008)
  10. A. Klimas, M. Hesse, S. Zenitani, and M. Kuznetsova, Particle-in-cell simulation of collisionless driven reconnection with open boundaries, Phys. Plasmas 17, 112904 (2010)
  11. M. Hesse, T. Neukirch, K. Schindler, M. Kuznetsova, and S. Zenitani, The Diffusion Region in Collisionless Magnetic Reconnection, Space Sci. Rev. 106, 3 (2011)
  12. A. Klimas, M. Hesse, and S. Zenitani, Particle-in-cell simulation of collisionless undriven reconnection with open boundaries, Phys. Plasmas 19, 042901 (2012)
  13. N. Aunai, M. Hesse, S. Zenitani, M. Kuznetsova, C. Black, R. Evans, and R. Smets, Comparison between hybrid and fully kinetic models of asymmetric magnetic reconnection: coplanar and guide field configurations, Phys. Plasmas 20, 022902 (2013)
  14. M. Hesse, N. Aunai, S. Zenitani, M. Kuznetsova, and J. Birn, Aspects of collisionless magnetic reconnection in asymmetric systems, Phys. Plasmas 20, 061210 (2013)
  15. T. Nagai, I. Shinohara, S. Zenitani, R. Nakamura, T. Nakamura, M. Fujimoto, Y. Saito, and T. Mukai, Three-dimensional structure of magnetic reconnection in the magnetotail from Geotail observations, J. Geophys. Res. 118, 1667 (2013a)
  16. T. Nagai, S. Zenitani, I. Shinohara, R. Nakamura, M. Fujimoto, Y. Saito, and T. Mukai, Ion and electron dynamics in the ion-electron decoupling region of magnetic reconnection with Geotail observations, J. Geophys. Res. 118, 7703 (2013b)
  17. T. Nagai, I. Shinohara, and S. Zenitani, Ion acceleration processes in magnetic reconnection: Geotail observations in the magnetotail, J. Geophys. Res. 120, 1766 (2015a)
  18. T. Nagai, I. Shinohara, and S. Zenitani, The dawn-dusk length of the X line in the near-Earth magnetotail: Geotail survey in 1994-2014, J. Geophys. Res. 120, 8762 (2015b)
  19. M. Hesse, N. Aunai, J. Birn, P. Cassak, R. Denton, J. F. Drake, T. Gombosi, M. Hoshino, W. Matthaeus, D. Sibeck, and S. Zenitani, Theory and Modeling for the Magnetospheric Multiscale Mission, Space Sci. Rev. 199, 577 (2016)
  20. H. Hasegawa, N. Kitamura, Y. Saito, ... S. Zenitani et al. (25th/26 author), Decay of mesoscale flux transfer events during quasi-continuous spatially-extended reconnection at the magnetopause, Geophys. Res. Lett. 43, 4755 (2016)
  21. T. K. M. Nakamura, S. Eriksson, H. Hasegawa, S. Zenitani, W. Li, K. Genestreti, R. Nakamura, and W. Daughton, Mass and energy transfer across the Earth's magnetopause caused by the vortex-induced reconnection, J. Geophys. Res. 122, 11505 (2017)
  22. T. K. M. Nakamura, W.-L. Teh, S. Zenitani, T. Umeda, M. Oka, H. Hasegawa, A. Veronig, and R. Nakamura, Spatial and time scaling of coalescing multiple magnetic islands, Phys. Plasmas 30, 022902 (2023)
  23. W.-L. Teh, T. K. M. Nakamura, S. Zenitani, T. Umeda, and R. Nakamura, New aspects of energy conversion in magnetic island dynamics: particle-in-cell simulation of multiple island coalescence and MMS observations, Astrophys. J. 947, 4 (2023)
  24. S. Usami and S. Zenitani, Three-dimensional crescent-shaped ion velocity distributions created by magnetic reconnection in the presence of a guide field, Phys. Plasmas 31, 022102 (2024)
  25. H. Hasegawa, M. R. Argall, ..., and S. Zenitani (36th/36 author), Advanced Methods for Analyzing In-Situ Observations of Magnetic Reconnection, Space Sci. Rev. 220, 68 (2024)
紀要（査読付）・解説記事
  1. M. Hesse, N. Aunai, M. Kuznetsova, S. Zenitani, and J. Birn, Magnetic Reconnection in Different Environments: Similarities and Differences, AGU Geophysical Monograph 207, 259 (2015)
  2. I. Shinohara, M. Fujimoto, T. Nagai, S. Zenitani, and H. Kojima, Low-frequency Waves in the Tail Reconnection Region, AGU Geophysical Monograph 216, 181 (2016)
  3. M. Yamada, J. Yoo, and S. Zenitani, Energy conversion and inventory of a prototypical magnetic reconnection layer, Astrophysics and Space Science Library 427, 143 (2016)
  4. 銭谷誠司, 磁気リコネクションにおけるプラズマ粒子軌道研究の進展, プラズマ・核融合学会誌 97, 47-55 (2021)
  5. 宇佐見俊介, 銭谷誠司, リコネクション研究の課題と将来: シミュレーション研究の課題と将来, プラズマ・核融合学会誌 89, 861-863 (2013)
その他資料


[もどる]

ＭＨＤリコネクションにおける圧縮性流体効果の研究

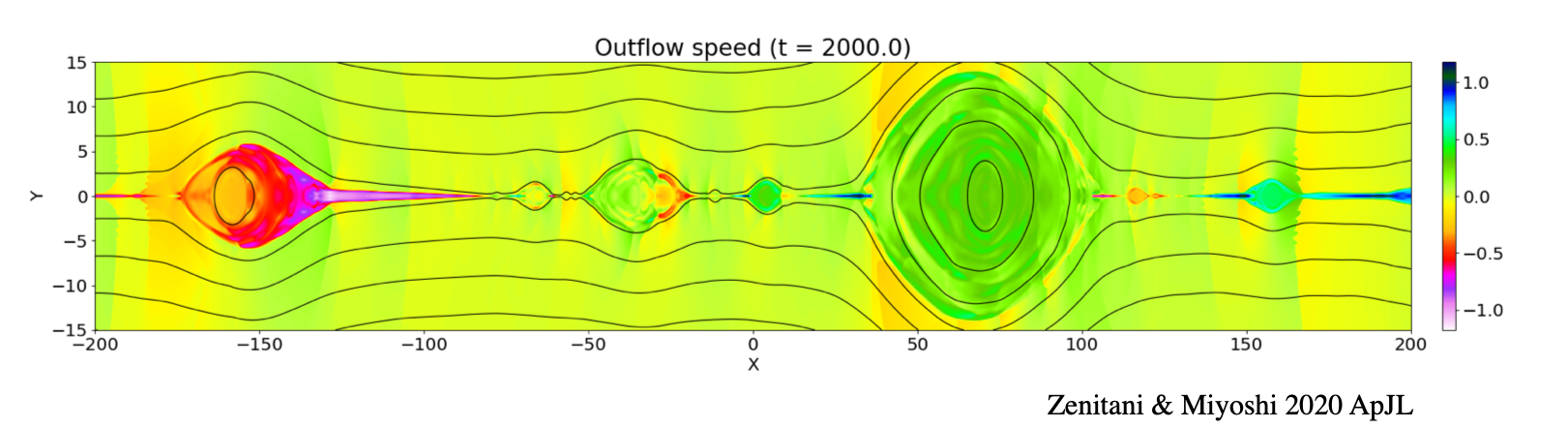
磁気リコネクションの MHD 理論は長年、非圧縮性を仮定した簡単な系で議論されてきました。 こうした簡略化は現象のエッセンスを掴むためには有用ですが、 太陽コロナなどのパラメーターでは、圧縮性を考慮した正確な議論が必要になります。 我々は、プラズマの圧縮性を考慮した定常リコネクションモデルを議論し、 エンタルピー流（内部エネルギーの流れ）がエネルギー収支で無視できないことを主張しています [4,5]。 また、典型的なプラズマβ（ガス圧と磁気圧の比）が低い環境では リコネクションジェットの速度が音速を超えるため、 圧縮性の影響が目に見える形で現れます。それは衝撃波です。 我々は、その頃、MHD 業界で広まりつつあった衝撃波捕捉型の数値解法に注目し、 新たにコードを書き起こしてシミュレーションを行いました。 その結果、リコネクションジェットの境界の Petschek スローショックの他に 遷音速／超音速流体に特有の衝撃波・不連続構造を作ることや [1,2]、 プラズマの圧縮効果によって乱流リコネクションのエネルギー変換効率が上がることがわかってきました [3]。

本研究 [1,2,3] で使ったシミュレーションコードは、それぞれ arXiv:1101.2255, 1503.01920, 2004.11247 （"Other formats" リンクを参照して下さい）からダウンロードすることができます。 さらに、これらのコードを発展させた OpenMHD コード およびその GPU 版を公開しています。OpenMHD とその派生コードは、国内外の多くの研究グループのシミュレーション研究で使われています（Nitta et al. 2016 ApJ, Shimizu et al. 2017 PoP [6], Teh & Zenitani 2021 ESS [11]）。

MHD reconnection

査読論文
  1. S. Zenitani and T. Miyoshi, Magnetohydrodynamic structure of a plasmoid in fast reconnection in low-beta plasmas, Phys. Plasmas 18, 022105 (2011)
  2. S. Zenitani, Magnetohydrodynamic structure of a plasmoid in fast reconnection in low-beta plasmas: Shock-shock interactions, Phys. Plasmas 22, 032114 (2015)
  3. S. Zenitani and T. Miyoshi, Plasmoid-dominated Turbulent Reconnection in a Low-β Plasma, Astrophys. J. Lett. 894, L7 (2020)
  4. M. Hesse, J. Birn, and S. Zenitani, Magnetic reconnection in a compressible MHD plasma, Phys. Plasmas 18, 042104 (2011)
  5. J. Birn, M. Hesse, and S. Zenitani, Reconnection in compressible plasmas: Extended conversion region, Phys. Plasmas 18, 111202 (2011)
  6. T. Shimizu, K. Kondoh, and S. Zenitani, Numerical MHD study for plasmoid instability in uniform resistivity, Phys. Plasmas 24, 112117 (2017)
  7. M. Hosseinpour, Y. Chen, and S. Zenitani, On the effect of parallel shear flow on the plasmoid instability, Phys. Plasmas 25, 102117 (2018)
  8. Y. Matsumoto, Y. Asahina, Y. Kudoh, T. Kawashima, J. Matsumoto, H. R. Takahashi, T. Minoshima, S. Zenitani, T. Miyoshi, and R. Matsumoto, Magnetohydrodynamic Simulation Code CANS+: Assessments and Applications, Publ. Astron. Soc. Japan 71, 83 (2019)
  9. W.-L. Teh and S. Zenitani, Thermodynamic Properties of Mirror Structures in the Magnetosheath: MMS Observations and Double-Polytropic MHD Simulations, Astrophys. J. 885, 22 (2019)
  10. W.-L. Teh and S. Zenitani, Thermodynamics of Dipolarization Fronts of Magnetic Reconnection in Anisotropic Plasma: MMS Observations and Resistive Double-polytropic MHD Simulations, Astrophys. J. 890, 114 (2020)
  11. W.-L. Teh and S. Zenitani, Two-Dimensional Reconstruction of a Time-Dependent Mirror Structure from Double-Polytropic MHD simulation, Earth and Space Science 8, e2020EA001449 (2021)
解説記事
  1. 銭谷誠司, 衝撃波対応コードを用いた磁気リコネクションの磁気流体シミュレーション研究, 生存圏研究 13, 27-33 (2017)
その他資料


[もどる]

プラズマ粒子シミュレーションの数値解法および解析手法の開発

プラズマ粒子（Particle-In-Cell; PIC）シミュレーションは、宇宙空間のさまざまな運動論プラズマ現象を再現・理解するために欠かせない研究ツールです。しかし、相対論的PICシミュレーション研究では、粒子の速度分布を生成したり、解析したりするための基盤アルゴリズムがそもそも整備されておらず、この分野の研究に取り掛かる障壁になっていました。 我々は、相対論的Maxwell（Maxwell-Juttner）分布や相対論的カッパ分布といった相対論的速度分布関数を乱数生成するアルゴリズム [1,4,6] と、体積要素の伸縮を損失なく扱うローレンツ変換アルゴリズム [1] を提案しました。2024年現在、[1] は多くの公開PICコード（EPOCH, Smilei, Tristan MP, WarpX）で採用されています。 これに関連して、ガンマ分布を乱数生成するアルゴリズム [7] や 相対論的粒子データを解析するための数理手法 [10] を提案しています。

今後、PICシミュレーションの規模はますます大きくなってゆきます。超大規模計算では計算誤差および負荷が累積しますから、個々の計算要素を高精度かつ高速に解くことがさらに重要になります。例えばPICシミュレーションの粒子計算部では Boris法（Boris 1970）という数値解法が広く使われていますが、Boris法は一定の誤差を生じることが知られています。そこで我々は、解析解や級数展開を使ってBoris法を高精度化したアルゴリズムを開発し続けています [2,3]。新手法は計算量が少し増えますが、PICシミュレーションでの性能低下も軽微ですし、相対論的高速プラズマ流で顕在化する数値問題を 1/3 に抑えることができます（Zenitani & Kato in prep.）。特に級数展開法 [3] は次世代の数値解法の基盤になると期待しています。

こうした解法そのものの性能向上に加えて、境界条件を工夫して実質的な計算サイズを大きくすることも必要です。我々の研究グループでは、PICシミュレーションの速度分布関数をより精緻に扱う開放境界条件を実装しました [8,9]。

PIC algorithms

査読論文
  1. S. Zenitani, Loading relativistic Maxwell distributions in particle simulations, Phys. Plasmas 22, 042116 (2015)
  2. S. Zenitani and T. Umeda, On the Boris solver in particle-in-cell simulation, Phys. Plasmas 25, 112110 (2018)
  3. S. Zenitani and T. N. Kato, Multiple Boris integrators for particle-in-cell simulation, Comput. Phys. Commun., 247, 106954 (2020)
  4. S. Zenitani and S. Nakano, Loading a relativistic Kappa distribution in particle simulations, Phys. Plasmas 29, 113904 (2022)
  5. S. Zenitani and S. Nakano, Loading Loss-Cone Distributions in Particle Simulations, J. Geophys. Res. 128, e2023JA031983 (2023)
  6. S. Zenitani, Modifications to Swisdak (2013)'s rejection sampling algorithm for a Maxwell-Jüttner distribution in particle simulations, Physics of Plasmas, 31, 094501 (2024)
  7. S. Zenitani, A gamma variate generator with shape parameter less than unity, Economics Bulletin, 44, 1113 (2024)
  8. A. Klimas, M. Hesse, and S. Zenitani, Particle-in-cell simulation of collisionless reconnection with open outflow boundaries, Phys. Plasmas 15, 082102 (2008)
  9. A. Klimas, M. Hesse, S. Zenitani, and M. Kuznetsova, Particle-in-cell simulation of collisionless driven reconnection with open boundaries, Phys. Plasmas 17, 112904 (2010)
  10. G. Ueno and S. Zenitani, Relativistic Maxwellian mixture model, Phys. Plasmas 28, 122106 (2021)
解説記事・研究ノートなど
  1. 銭谷誠司, 加藤恒彦, 相対論的プラズマ粒子シミュレーションのための粒子計算アルゴリズム, 生存圏研究 14, 62-77 (2018)
  2. T. N. Kato and S. Zenitani, Volume-preserving particle integrator based on exact flow of velocity for nonrelativistic particle-in-cell simulations, arXiv:2108.02426 (2021)
  3. S. Zenitani, A note on the flattop velocity distribution in space plasmas, Research Notes of the AAS 8, 30 (2024)
その他資料


[もどる]

相対論ジェットの異常加速過程の研究

活動銀河核やガンマ線バースト (GRB) などで考えられている相対論ジェットについて、近年、活発にシミュレーション研究が進んでいます。こうした中、相対論的速度で吹き出すジェットと外側の静止プラズマとの境界領域で、ジェットの膨張に伴う希薄波領域で、これまで知られていなかった流体加速（異常加速）が起きることが報告されました（Aloy & Rezzolla 2006 ApJ）。我々は、１次元 RMHD シミュレーションで異常加速現象を再現し、これが相対論完全流体近似のもとで現れる断熱加速の１種であることを示しました。

査読論文
  1. S. Zenitani, M. Hesse, and A. Klimas, Scaling of the Anomalous Boost in Relativistic Jet Boundary Layer, Astrophys. J. 712, 951-956 (2010)
講演資料


[もどる]

都市デジタルツインのためのデータ取り込み技術の研究

神戸大学都市安全研究センターは、仮想空間内に 都市のデジタルツイン（デジタル世界での双子という意味です）を用意して、 地震や津波などの巨大災害に対する防災シミュレーションに役立てる「都市丸ごとシミュレーション」を構想しています。 都市デジタルツインを作成するためには、設計図などから構造物の外形・素材データを取り込む必要があり、 そのための技術開発が必要になります。 比較的新しい構造物であれば、設計図のCADファイルを取り込むことができます。 しかし、20世紀に造られた構造物の設計図は手書き図面であることが多いため、 図面のスキャン画像からデータを取り込まなければなりません。 私たちは、画像解析技術、特に最近進展が著しい深層学習（ディープラーニング）技術を使って、 図面からデータを取り込む技術を開発しています [1]。 また、こうした深層学習をより効率的に進めるために、 ニューラルネットワーク内部で用いる新しい数値解法を開発しています（Zenitani, in prep.）。

CC BY-SA 4.0; https://en.wikipedia.org/wiki/Computer_vision  

研究報告
  1. 名下宥佑、銭谷誠司、SSD アルゴリズムによる画像認識技術を用いた図面要素抽出の研究、関西ジオシンポジウム 2022 論文集, 91-96 (2022)
  2. 出口直輝、銭谷誠司、名下宥佑、桝谷英弥、ディープラーニングによる物体検知技術YOLOv5を用いた図面要素抽出の研究、都市安全研究センター研究報告 26, 20 (2022)
  3. 陳冉、竹山智英、銭谷誠司、橘伸也、飯塚敦、機械学習による過圧密比の深度分布推定、都市安全研究センター研究報告 25, 33 (2021)
  4. 堂ヶ原健、竹山智英、銭谷誠司、橘伸也、飯塚敦、地盤応答解析コードの GPU 並列化、都市安全研究センター研究報告 26, 10 (2022)


[もどる]

公開コード

OpenMHDコード
p++コード

推薦書籍など

書籍
学会誌など（PDFファイル）
YouTube, TV channel
ウェブページ

戻りましょう