OpenMHD は Modern Fortran & CUDA Fortran で書かれた 磁気流体 (MHD) シミュレーションコードです。 シンプルな実装で動作が軽く、 Python/IDL の解析・可視化ルーチンを同梱しているため、 計算実行から可視化までを手軽に体験できるようになっています。 シリアル版、MPI/OpenMP並列版、GPU版、MPI/GPU版を同梱していますので、 PCでもスーパーコンピューターでも同じコードを走らせることができます。
OpenMHD コードは、作者の MHD リコネクション研究 [1,2] の並列コードをパッケージ化したものです。 そして、その後の改良を取り入れて、随時更新を続けています。
ファイル
tar.gz ファイルを直接ダウンロードしてください。
- 安定版 (2025/08/04)
開発中のコードは GitHub で管理しています。以下のように git コマンドでリポジトリを複製します。
$ git clone https://github.com/zenitani/OpenMHD.git
動作環境
動作を確認している環境は以下の通りです。 あまり凝ったことをしていないので、ほとんどの環境で動作するはずです。 MPI 並列計算には、MPI-3.1 規格に準拠したMPIライブラリが必要です。
- コンパイラ
- Intel oneAPI HPC Toolkit
- AMD Optimizing C/C++ and Fortran Compilers (AOCC)
- gfortran 12.1
- Cray Fortran コンパイラ
- NVIDIA HPC SDK: nvfortran 21.7以降
- MPIライブラリ(オプション)
- 可視化環境(オプション)
- Python 3 + Matplotlib
- IDL 8.5
基礎方程式と計算手法
次のような保存形の磁気流体方程式を採用しています。 \begin{align} \frac{\partial \rho}{\partial t} &+ \nabla \cdot ( \rho \vec{v} ) = 0, \\ \frac{\partial \rho \vec{v}}{\partial t} &+ \nabla \cdot ( \rho\vec{v}\vec{v} + p_T\overleftrightarrow{I} - \vec{B}\vec{B} ) = 0, \\ \frac{\partial \mathcal{E}}{\partial t} &+ \nabla \cdot \Big( (\mathcal{E}+p_T )\vec{v} - (\vec{v}\cdot\vec{B}) \vec{B} + \eta \vec{j} \times \vec{B} \Big) = 0, \\ \frac{\partial \vec{B}}{\partial t} &+ \nabla \cdot ( \vec{v}\vec{B} - \vec{B}\vec{v} ) + \nabla \times (\eta \vec{j}) + \nabla \psi = 0, \\ \frac{\partial \psi}{\partial t} &+ c_h^2 \nabla \cdot \vec{B} = - \Big(\frac{c_h^2}{c_p^2}\Big) \psi, \end{align} このうち、$p_T=p+B^2/2$ は磁気圧を含めた総圧、 $\overleftrightarrow{I}$ は単位テンソル、 $\mathcal{E}=p/(\Gamma-1) + \rho v^2/2 + B^2/2$ はエネルギー密度、 $\Gamma=5/3$ は断熱定数です。 これらの式は $4\pi$ や $\mu_0$ などの係数が消える Lorentz-Heaviside 風の表式を使っています。 音速は $c_s \equiv \sqrt{\Gamma p / \rho }$、アルヴェン速度は $c_A \equiv B / \sqrt{\rho}$ になります。
$\psi$ は計算結果を補正するための仮想ポテンシャルです。 本来、磁場はソレノイダル条件 $\nabla \cdot \vec{B} = 0$ を満たしますが、 シミュレーションでは数値エラーで $\nabla \cdot \vec{B} \ne 0$ となることがあります。 そうすると、磁気トポロジーが変わるだけでなく 磁気単極子に対して非物理的な力が働いて計算結果を壊してしまいます。 そこで、仮想ポテンシャル $\psi$ を介して $\nabla \cdot \vec{B}$ の数値エラーを 拡散・減衰させます(Hyperbolic divergence cleaning 法 [3])。 $c_h,c_p$ は拡散・減衰度合いを調整するパラメーターです。
OpenMHD コードは、数値流束を評価する際に、 隣接するセル境界での一次元リーマン問題を考える近似リーマン解法を使っています。 その中でも5種類の不連続面に対応した HLLD 法 [4] を採用しています。 HLLD 法は、リーマン問題を適度な計算コストで精度良く近似するため、 MHD シミュレーションでは非常によく使われています。 本稿執筆(2026年)時点では業界標準と言って良いでしょう。
コードの計算精度は時間・空間ともに2次精度です。 2段の Runge=Kutta 法あるいは TVD Runge=Kutta 法で時間発展を解くとともに、 物理量(基本量)を MUSCL 補間して2次の空間精度を達成しています。 ψのソース項は、Runge=Kutta 部分の前後で 0.5Δt ずつ、 解析解 $\psi = \psi_0 \exp [ - ({c_h^2}/{c_p^2}) t ]$ を解いています。 他の技術的な詳細は、文献 [1,2] 及びその参考文献を参照してください。 OpenMHD を取り巻く研究状況については「生存圏研究」の記事 [5] を参照してください。
参考文献
- S. Zenitani & T. Miyoshi, Phys. Plasmas 18, 022105 (2011)
- S. Zenitani, Phys. Plasmas 22, 032114 (2015)
- A. Dedner et al., J. Comput. Phys. 175, 645 (2002)
- T. Miyoshi & K. Kusano, J. Comput. Phys. 208, 315 (2005)
- 銭谷誠司、生存圏研究 13, 27 (2017)
参考資料
- 超並列磁気流体シミュレーションコード OpenMHD-GPU の開発 (PDF 9.7MB; 天文学会2022春季年会講演資料)
- OpenMHD: Godunov-type code for magnetic reconnection and MHD problems (PDF 14MB)
- Magnetohydrodynamic (MHD) simulations (PDF 12.2MB; Lecture at International School for Space Simulations; ISSS-15, 2024)
- Introduction to magnetohydrodynamic simulations (PDF 13.7MB; Lecture at NAOJ 2014/2015)
OpenMHD の使い方は以下の通りです。
- はじめよう
- 解析・可視化(Python/IPython)
- 解析・可視化(Python/Jupyter)
- 解析・可視化(IDL)
- 解析・可視化(gnuplot/Mathematica)
- ムービーの作成方法(Python/Pillow)
- ムービーの作成方法(Python/OpenCV)
- ムービーの作成方法(ImageMagick)
- ムービーの作成方法(FFmpeg)
Google Colaboratoryのアカウントをお持ちの方は、クラウド上で計算・データ解析を試すことができます。
- CPU版ノートブック (Google Colab)
- GPU版ノートブック (Google Colab)
はじめよう
OpenMHD ウェブページのトップから tar.gz ファイルをダウンロードしてください。 そして、ダウンロードしたファイルを tar コマンドで解凍すると、 たくさんのディレクトリと関連ファイルが展開されます。 (以下の操作には、Linux/macOS のターミナル環境が必要です。 Windows では、ディレクトリの中に含まれているUNIXのシンボリックリンクをうまく扱うことができません。)
$ gunzip openmhd-20250804.tar.gz $ tar xvf openmhd-20250804.tar
しかるべきディレクトリに移動します。
手始めに 2D_basic ディレクトリに移動してみましょう。
$ cd openmhd-20250804/2D_basic/
OpenMHD は UNIX の
make コマンドを使って、
ソースコードをコンパイルします。
まず、テキストエディタで Makefile というファイルを開いて、
F90 という変数を書き換えてコンパイラを指定してください。
MPI並列計算を行う場合は、MPI用の fortran コンパイラを指定します。
シリアル版のみを利用する場合は、普通の fortran コンパイラを指定するだけで良いでしょう。
F90 = gfortran
そして、make コマンドでプログラムをコンパイルします。
$ make
OpenMHD の2次元問題には MPI 並列コードが同梱されています。 デフォルトでは、シリアル版と並列版の両方をコンパイルします。 シリアル版だけをコンパイルするのであれば、
$ make run
だけでも OK です。
このあたりのルールは Makefile の中身を参照してください。
無事コンパイルが終われば、
シリアル版の実行ファイル(a.out)および
MPI 並列版の実行ファイル(ap.out)ができているはずです。
次にプログラムを走らせてみましょう。 シリアル版の場合は、コマンドラインで直接実行ファイルを指定します。
$ ./a.out
あるいは
$ ./a.out | tee output.log
とします。 UNIXでは自分が今いるディレクトリ(カレントディレクトリ)を "." と表しますが、 "a.out" ではなく "./a.out" と書くことで、 カレントディレクトリの a.out ファイルを実行することを明示しています。 UNIXの tee コマンドは、プログラムの(標準)出力を画面に表示しつつ、ファイル(output.log)に記録します。
MPI 並列版を使う場合は、メインファイル(例:mainp.f90)先頭付近の
mpi_nums 変数を編集してプロセス数を指定してください。
計算領域を 4 x 1 に分割する場合は (/4, 1/)、
2 x 2 に分割する場合は (/2, 2/) のようにします。
mpi_nums(2) の (2) の部分は
2次元を意味していますので変える必要はありません。
integer, parameter :: mpi_nums(2) = (/4, 1/) ! MPI numbers
make コマンドでプログラムをコンパイルした後、
mpirun コマンドを使って実行ファイルを走らせます。
その際、-np オプションで並列プロセス数 4 を指定します。
このプロセス数は mpi_nums 変数で指定したプロセス数と一致させてください。
$ mpirun -np 4 ./ap.out $ mpirun -np 4 ./ap.out | tee output.log
計算が終了すると、data/ ディレクトリに結果が出力されています。
$ ls data/ field-00000.dat field-00007.dat field-00014.dat field-00021.dat field-00028.dat field-00035.dat field-00001.dat field-00008.dat field-00015.dat field-00022.dat field-00029.dat field-00036.dat field-00002.dat field-00009.dat field-00016.dat field-00023.dat field-00030.dat field-00037.dat field-00003.dat field-00010.dat field-00017.dat field-00024.dat field-00031.dat field-00038.dat field-00004.dat field-00011.dat field-00018.dat field-00025.dat field-00032.dat field-00039.dat field-00005.dat field-00012.dat field-00019.dat field-00026.dat field-00033.dat field-00040.dat field-00006.dat field-00013.dat field-00020.dat field-00027.dat field-00034.dat
スーパーコンピューターでは、
qsub, qstat などのコマンドを使って、
計算ノードにジョブを投入することが多いと思います。
こうしたジョブ投入系のコマンドの使い方は、
それぞれのスパコンシステムの利用マニュアルを参照してください。
無事、計算が実行できたら、計算結果をプロットして確認してみましょう。 OpenMHD では、各物理課題ごとに Python (Matplotlib) と IDL の可視化ルーチンを用意しています。 Python は、IPython・Jupyter の2通りの解析・可視化方法に対応しています。
解析・可視化(Python/IPython)
Python で解析・可視化する方法はいくつかありますが、
我々は IPython を使うことをお勧めします。
まず、ipython3 コマンドで作業用の IPython シェルを起動します。
すると、In [番号] の形式のプロンプトが表れます。
$ ipython3 --pylab
Python 3.14.3 (v3.14.3:323c59a5e34, Feb 3 2026, 11:41:37) [Clang 16.0.0 (clang-1600.0.26.6)]
Type 'copyright', 'credits' or 'license' for more information
IPython 9.10.0 -- An enhanced Interactive Python. Type '?' for help.
Using matplotlib backend: macosx
In [1]:
次にサンプルスクリプト(plot.py)を実行してみます。
%run -i は IPython のコマンドで、"%" から入力します。
-i オプションはファイルを interactive モードで実行することを意味しています
(参考:IPython tutorial)。
なお、plot.py を途中まで入力してタブキーを押すと、
IPython が plot.py を含む候補名を補完してくれます。
このようなファイル名補完は IPython の便利な機能の1つです。
In [2]: %run -i plot.py
これを実行すると、下のようなプロット画面が現れるはずです。
もし画面が現れなければ、plt.show() で明示的に表示させてください。
In [3]: plt.show()
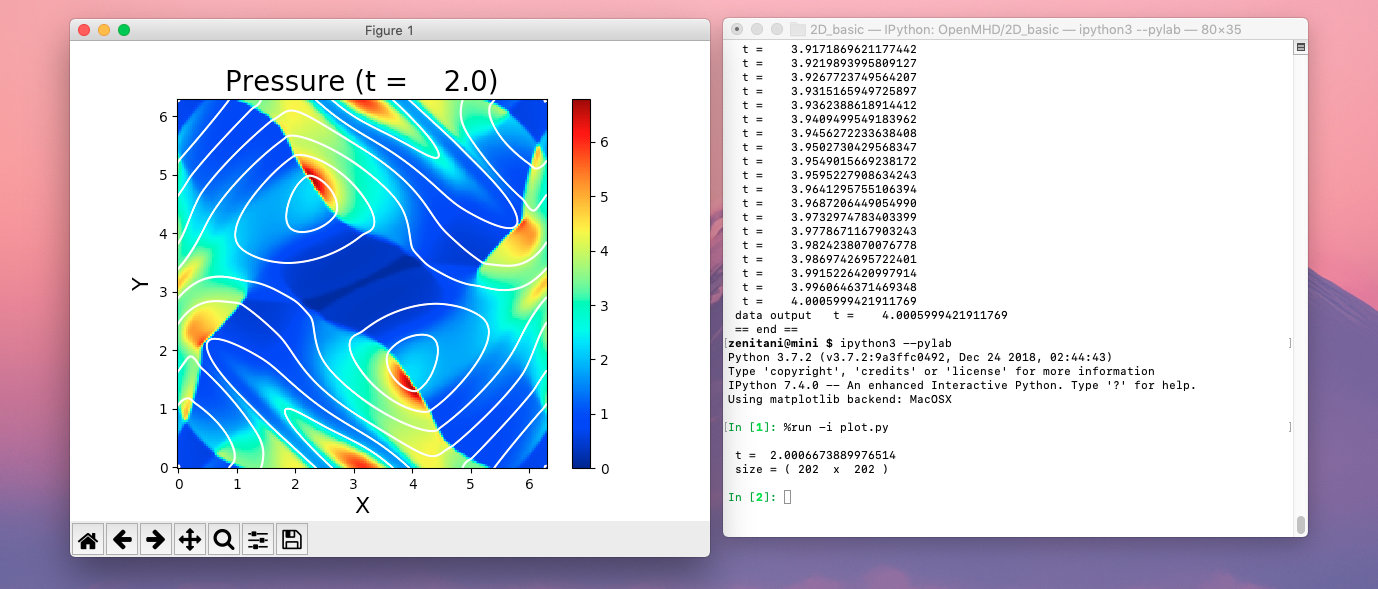
プロットの作成方法は plot.py ファイルに
Python 言語で記述されていますので、
興味のある方は見てみてください。
このうち、ファイル冒頭の
import openmhd
のところで、OpenMHD データファイル用のライブラリを読み込んでいます。
このライブラリの本体はシンボリックリンクを辿った先の
visualization/python/openmhd.py にあり、
以下の2種類のサブルーチンを提供しています。
data_readdata_read_from_bigendian
そして、以下の箇所で
データファイル(field/data-00020.dat)を指定して読み込んでいます。
x, y は位置座標の配列、
t は時間、そして、
data が物理量の配列です。
# reading the data ...
x,y,t,data = openmhd.data_read("data/field-00020.dat")
同じルーチンに ix1, ix2, jx1, jx2(配列の添字番号)や
xrange, yrange(座標の範囲)などのオプション引数を渡すと、
データの読み込み範囲を絞り込むことができます。
# reading the data (partial domain: [ix1,ix2] x [jx1,jx2])
x,y,t,data = openmhd.data_read("data/field-00020.dat",ix1=0,ix2=100,jx1=11)
x,y,t,data = openmhd.data_read("data/field-00020.dat",xrange=[0.0,3.14159],yrange=[0.0,3.14159])
実行環境(スパコン)と解析環境(PC等)でエンディアンが違う場合は、
Python側でエンディアンを変換することができます。
Little endian 環境で Big endian データを読み込む場合は、
data_read_from_bigendian ルーチンを使ってください。
エンディアン変換以外の動作は data_read と同じです。
読み込んだデータの配列(data[ix,jx,9])は、サイズが ix, jx, 9 の3次元配列になっていて
最後の次元が物理量を表しています。
例えばプラズマ圧力は data[:,:,3] に入っていますが、
ファイル冒頭のダミー変数を使って data[:,:,pr] とするとわかりやすいでしょう。
ダミー変数の最後の ps は、$\nabla \cdot \vec{B}$ 問題対策の仮想ポテンシャルψです。
(「はじめに > 基礎方程式と計算手法」を参照)
IPython シェルでは、引き続きこれらのデータとプロットを操作することができます。 例えば、以下のようにするとカラーバーが赤=青色に変わります。
In [4]: myimg.set_cmap('RdBu_r')
画像をたくさん出力して、1つのムービーにまとめることもできます。
2次元渦問題(2D_basic)には、
ムービー作成用のサンプルファイル(plot_movie.py)を用意しています。
このサンプルでは、以下のループをまわして連番ファイルを作ります。
その際、movie というディレクトリを自動生成しますがご了承ください。
In [5]: %run -i plot_movie.py
他の物理問題の場合は、このサンプルを参考にスクリプトを用意してください。
# ---- loop for movies ---------------
for ii in range(0,41):
# reading the data ...
x,y,t,data = openmhd.data_read(ii)
Python の range(0,41) は 0,1,...40 を表すことに注意しましょう。
実行し終えたら movie/ ディレクトリの中を確認してみましょう。
$ ls movie/ output-00000.png output-00011.png output-00022.png output-00033.png output-00001.png output-00012.png output-00023.png output-00034.png output-00002.png output-00013.png output-00024.png output-00035.png output-00003.png output-00014.png output-00025.png output-00036.png output-00004.png output-00015.png output-00026.png output-00037.png output-00005.png output-00016.png output-00027.png output-00038.png output-00006.png output-00017.png output-00028.png output-00039.png output-00007.png output-00018.png output-00029.png output-00040.png output-00008.png output-00019.png output-00030.png output-00009.png output-00020.png output-00031.png output-00010.png output-00021.png output-00032.png
そして、次の4つの方法のどれかを使って、 バラバラの画像ファイルを1つのムービーにまとめます。
解析・可視化(Python/Jupyter)
Jupyter ノートブック でも、 Python でデータを解析することができます。 Jupyter がインストールされていない場合は、 pip3 で jupyter および ipywidgets ライブラリをインストールしてください。 (ipywidgets は後述のインタラクティブ機能を使うために必要です。これがなくてもその他の基本機能を使うことができます)
$ pip3 install jupyter ipywidgets [ $ pip3 install -U jupyter ipywidgets ]
コマンドラインで次のコマンドを実行すると、 ブラウザの画面で Jupyter ノートブックを見ることができます。
$ jupyter-notebook plot.ipynb
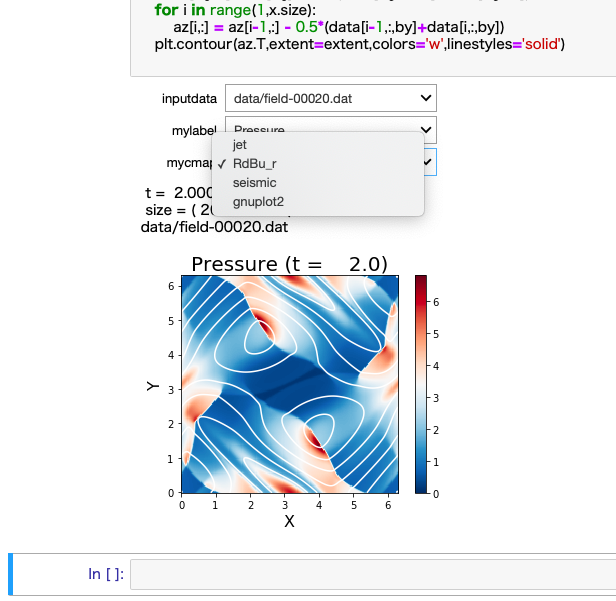
そして、セルを選択して Shift + Enter キーを押すと、
セル内の Python プログラムを実行することができます。
プロット画像はノートブックの中にインライン表示されます。
Python プログラムの中身は、
解析・可視化(Python/IPython) で紹介したものと同じものです。
2次元渦問題(2D_basic)のノートブックには、
ムービー作成用のサンプルスクリプトも用意しています。
最後に jupyter-notebook コマンドを実行したターミナルで Ctrl + C キーを押すと、Jupyter を終了させることができます。
解析・可視化(IDL)
idl コマンドで IDL を立ち上げます。
IDL> が IDL のプロンプトです。
$ idl IDL 8.7.2 (darwin x86_64 m64). (c) 2019, Harris Geospatial Solutions, Inc. Licensed for use by: Kobe University - Zenitani License: ***-******* IDL>
以下のように .r コマンドでバッチファイル(batch.pro)を実行してみましょう。
IDL> .r batch
下のようなプロット画面が現れるはずです。
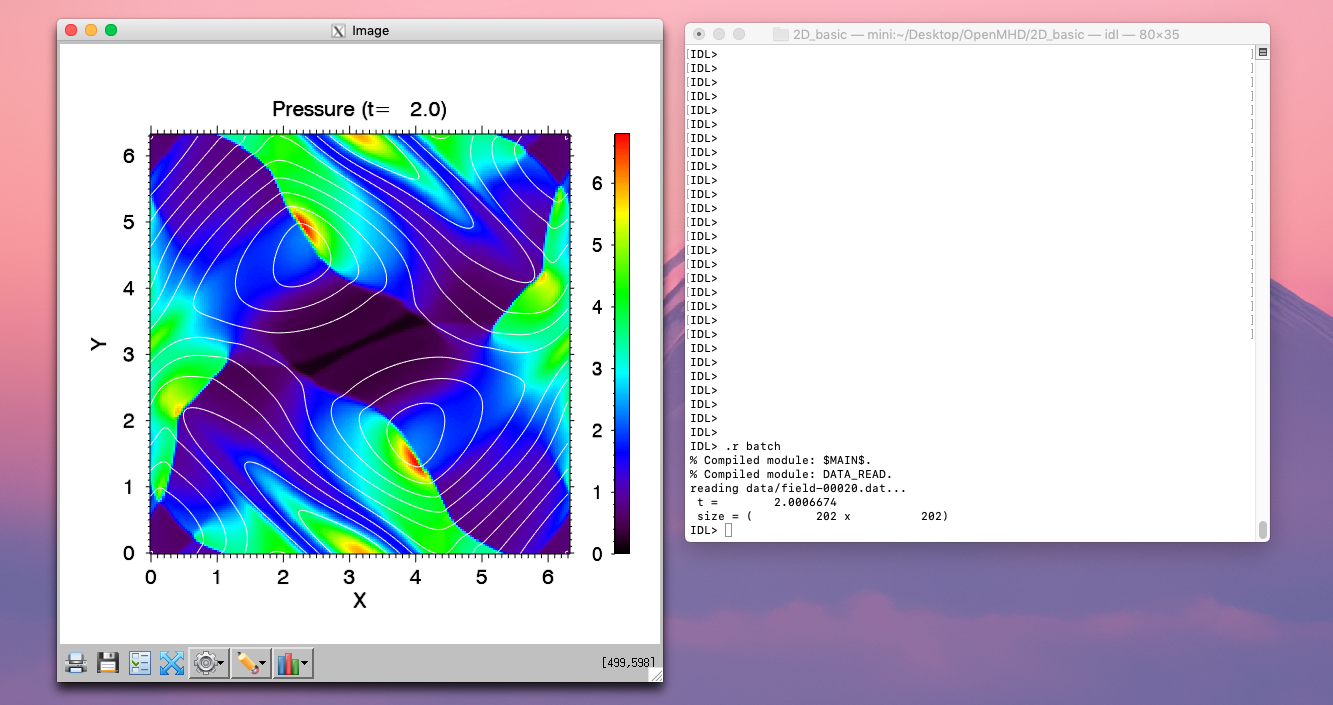
プロットの生成方法は batch.pro ファイルの中に IDL 言語で記述されています。
興味のある方はぜひ見てみてください。
ファイル冒頭の以下の部分で、OpenMHD 専用のルーチンを読み込んでいます。
サブルーチンファイルはシンボリックリンクを辿った先の visualization/idl/data_read.pro にあります。
;; find and compile data_read routine resolve_routine, "data_read"
そして、適当なデータファイル(field/data-00020.dat)を読み込みます。
x, y は位置座標の配列、
t は時間、そして、
data が物理量の配列です。
;; reading the data ... data_read,data,x,y,t,'data/field-00020.dat'
同じルーチンに ix1, ix2, jx1, jx2(配列の添字番号)や
xrange, yrange(座標の範囲)などのオプション引数を渡すと、
データの読み込み範囲を絞り込むことができます。
;; reading the data (partial domain: [ix1,ix2] x [jx1,jx2]) data_read,data,x,y,t,'data/field-00020.dat',ix1=0,ix2=100,jx1=11 data_read,data,x,y,t,'data/field-00020.dat',xrange=[0.0,3.14159],yrange=[0.0,3.14159])
実行環境(スパコン)と解析環境(PC等)でエンディアンが違う場合は、
data_read.pro ファイルの中の openr 関数に
/swap_endian キーワードを追加して、
データ読み込み時にエンディアンを変換して下さい。
; no record marker
openr,/get_lun,unit,filename,/swap_endian
読み込んだデータの配列は3次元配列になっていて、
最後の次元が物理量を表しています。
例えばプラズマ圧力は data[*,*,3] に入っていますが、
冒頭のダミー変数を使って data[*,*,pr] のように書くとわかりやすいです。
ムービーを作る場合は、サンプルファイル(batch_movie.pro)を参考に大量の画像を出力すれば良いでしょう。
IDL> .r batch_movie
このファイルを実行し終えると、Python の場合と同様、movie/ ディレクトリの中に画像ファイルができています。
$ ls movie/ output-00000.png output-00011.png output-00022.png output-00033.png output-00001.png output-00012.png output-00023.png output-00034.png output-00002.png output-00013.png output-00024.png output-00035.png output-00003.png output-00014.png output-00025.png output-00036.png output-00004.png output-00015.png output-00026.png output-00037.png output-00005.png output-00016.png output-00027.png output-00038.png output-00006.png output-00017.png output-00028.png output-00039.png output-00007.png output-00018.png output-00029.png output-00040.png output-00008.png output-00019.png output-00030.png output-00009.png output-00020.png output-00031.png output-00010.png output-00021.png output-00032.png
そして、次のどれかの方法で、 バラバラの画像ファイルを1つのムービーにまとめます。
解析・可視化(gnuplot/Mathematica)
OpenMHD の計算結果は、データ形式さえ合えば Python/IDL 以外の言語・ツールでも可視化できるはずです。可視化ルーチンの開発に役立ちそうな情報を挙げておきます。
- 和田智秀さんが提供してくださった gnuplot のサンプルコードを
OpenMHD の配布ファイルの
visualization/gnuplotに収録しています。 - Mathematica でデータを読み込むサンプルを こちら に置いています。
ムービーの作成方法(Python/Pillow)
Python の画像処理ライブラリ Pillow を使うと、
上記の2次元課題で生成した画像ファイルを
1つのアニメーション GIF ファイルに変換することができます。
まず、pip で Pillow をインストールします。
$ pip3 install pillow [あるいは $ pip install pillow]
そして、以下のスクリプトを IPython などで実行します。 インポート先のパッケージ名が Pillow でなく PIL になっていますので、ご注意ください。
import glob
from PIL import Image
images = []
for png in sorted(glob.glob("movie/output-*.png")):
im = Image.open(png)
images.append(im)
images[0].save('animation_pillow.gif', save_all=True, append_images=images[1:], optimize=False, duration=100, loop=0)
最後の save() メソッドの duration オプションの数字は、各コマの表示時間(ミリ秒)です。 これを変更すると、動画の再生速度を変更することができます。
その他の詳細は、以下のページを参考にしてください。
ムービーの作成方法(Python/OpenCV)
コンピュータビジョンライブラリ OpenCV の Python インターフェースを使うと、
バラバラの画像ファイルを MP4 ムービーに変換することができます。
インストール方法はいろいろありますが、
例えば、pip で opencv-python をインストールすれば良いでしょう。
$ pip3 install opencv-python [あるいは $ pip install opencv-python]
そして、以下のスクリプトを IPython などで実行します。
このサンプルはノートブックファイル(plot.ipynb)に含まれているはずです。
OpenCV のパッケージ名は cv2 です。
import glob
import cv2
images = []
for png in sorted(glob.glob("movie/output-*.png")):
im = cv2.imread(png)
height, width, layers = im.shape
images.append(im)
out = cv2.VideoWriter("animation_cv2.mp4", cv2.VideoWriter_fourcc(*'MP4V'), 10.0, (width, height))
for i in range(len(images)):
out.write(images[i])
out.release()
cv2.VideoWriter の2つめの引数はコーデック、
3つめの引数は動画の再生レート(fps)、
4つめは動画の大きさ(横・縦)です。
fps の数値を変えて、動画の再生速度を調整することができます。
その他の詳細は、以下のページを参考にしてください。
- 複数の画像から動画ファイルを作る - 株式会社ファントム
- Getting Started with Videos - OpenCV-Python Tutorials
- 動画を保存する - OpenCV-Python チュートリアル
ムービーの作成方法(ImageMagick)
ImageMagick で
画像ファイルを1つにまとめることができます。
次のコマンドは、上記の2次元課題で生成した movie/ ディレクトリの画像ファイルをアニメーション GIF に出力します。
$ convert movie/output-000*.png result.gif
出力するムービーの形式は、ファイル名の拡張子によって自動判別されます。 例えば
$ convert movie/output-000*.png result.mp4
とすると MPEG4 ムービーを生成できます。 後者の MPEG4 変換機能は後述の FFmpeg を呼び出しているため、FFmpeg のある環境で使えます。
Ubuntu Linux では、これらのツールを以下のようにしてインストールできます。
$ sudo apt install imagemagick $ sudo apt install imagemagick ffmpeg
参考ページ:
ムービーの作成方法(FFmpeg)
FFmpeg でも同様に、
バラバラの画像ファイルを1つにまとめることができます。
次のコマンドは、movie/ ディレクトリの画像ファイルを MPEG4 ムービーに出力します。
GIF アニメーションの場合と比べるとファイルサイズはかなり小さくなります。
(一方、少し画質も荒くなります)
$ ffmpeg -i movie/output-%05d.png result.mp4
-r オプションで
ムービーの再生レートを調整することができます。
$ ffmpeg -r 10 -i movie/output-%05d.png -r 10 result.mp4
Ubuntu Linux では、以下のようにして FFmpeg をインストールします。
$ sudo apt install ffmpeg
参考ページ:
いちばん利用者の多い磁気リコネクション課題を例に説明します。
以下は 2D_reconnection ディレクトリの下のファイル一覧です。
一部のファイルはシンボリックリンクになっていますが、
基本的に必要なファイルは同じディレクトリの中から見えるはずです。
ユーザーは * のファイルを編集してプログラムをコンパイル・計算を実行します。
黄色・青色背景のファイルは可視化・解析用のファイル群です。
同様に、ユーザー側で * のファイルを編集してください。
磁気リコネクション課題にはシリアル版・並列版の2つのサンプルが収録されています。 それぞれについて、メインファイル、初期条件、境界条件ファイルと Makefile のコンパイル手順を用意しています。 コードをコンパイルする場合は、以下のようにしてください。
$ make run (シリアル版) $ make runp (並列版)
| ファイル名 | 内容 | |
| Makefile | * | コンパイルの手順書 |
| batch.pro | * | IDL の可視化ルーチン |
| bc.f90 | * | 境界条件(シリアル版) |
| data/ | データディレクトリ | |
| data_read.pro | IDL のサブルーチン(データ読み込み部) | |
| fileio.f90 | ファイル入出力(シリアル版) | |
| flux_resistive.f90 | * | 電気抵抗の設定と数値流束の計算(その2) |
| flux_solver.f90 | 数値流束の計算(その1:LLF/HLL/HLLC/HLLD 法による主要部分) | |
| glm_ss2.f90 | ソース項(div B 対策の仮想ポテンシャル ψ) | |
| limiter.f90 | Slope limiter:空間方向に物理量を補間する | |
| main.f90 | * | メインファイル(シリアル版) |
| mainp.f90 | * | メインファイル(並列版) |
| model.f90 | * | 初期条件(シリアル版) |
| modelp.f90 | * | 初期条件(並列版) |
| mpibc.f90 | * | 境界条件(並列版) |
| mpiio.f90 | ファイル入出力(並列版) | |
| openmhd.py | Python3 のサブルーチン(データ読み込み部) | |
| parallel.f90 | 並列通信モジュール | |
| param.h | 比熱比、配列番号 | |
| plot.ipynb | * | Python3 可視化ルーチンの Jupyter notebook |
| plot.py | * | Python3 可視化ルーチン |
| rk.f90 | Runge-Kutta 法コード | |
| set_dt.f90 | 時間ステップの設定 | |
| u2v.f90 | 保存量 (U) から基本量 (V) への変換 |
配布ファイルには、以下の物理課題を収録しています。 対応するディレクトリ名を(括弧)で示しています。
- 1次元リーマン問題
(1D_basic) - 相対論ジェット境界層の異常加速問題
(1D_relativisticJet) - 2次元渦問題
(2D_basic) - Kelvin-Helmholtz 不安定
(2D_KH) - 磁気リコネクション
(2D_reconnection,3D_reconnection) - 3次元磁気ループ移流問題
(3D_basic)
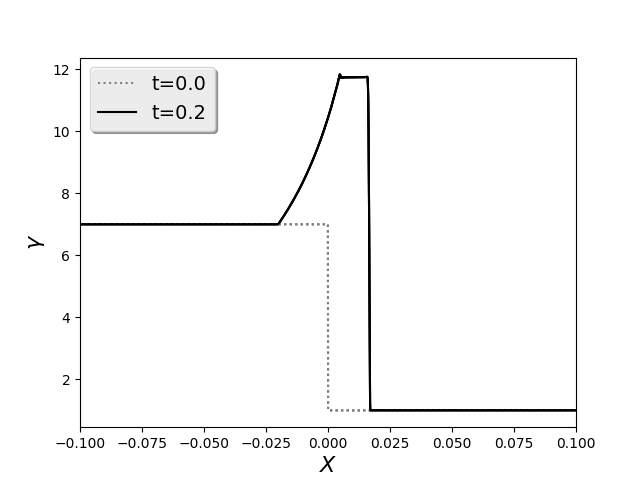
1次元リーマン問題
1次元リーマン問題は、ある境界(x=0.0)の左右に別々の状態を設定した後で、
次の瞬間に手を離し、系の時間発展を見る基本問題です。
このとき、系は複雑な構造を伴いながら、自己相似的に広がっていきます。
そもそも OpenMHD は、セル境界でリーマン問題を考慮するリーマンソルバーを採用しているわけですから、リーマン問題はコードの精度に直結する最重要テスト問題です。
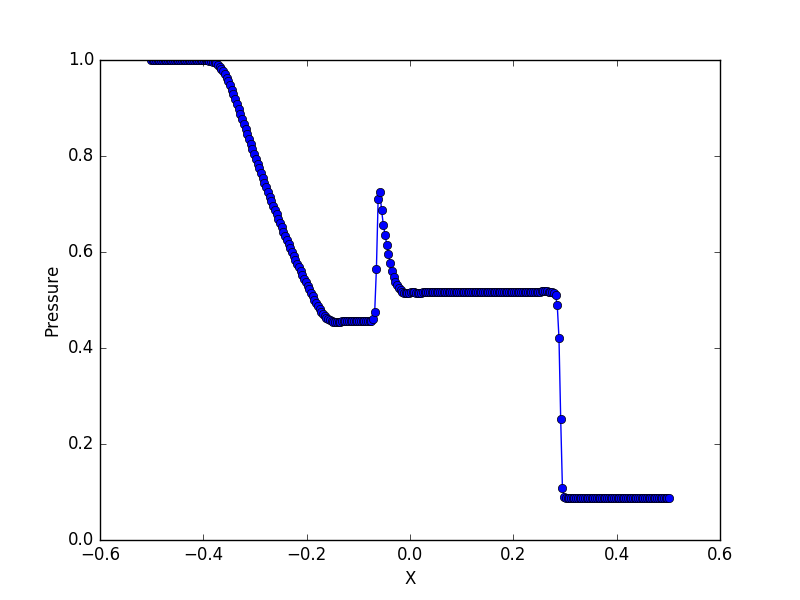
初期設定ファイル(model.f90)には、典型的なテスト問題のパラメーターが収録されています。下の図は、Brio & Wu (1988) で議論されている複合波問題です。
基本問題のいくつかは比熱比 Γ=2 で計算します。必要であれば、パラメーターファイル(param.h)の変数 gamma を変更してください。また、param.hファイルはコード全体で共有されていますので、後で Γ=5/3 に戻すのを忘れないでください。
相対論ジェット境界層の異常加速問題
活動銀河核やガンマ線バースト (GRB) では、相対論的速度でジェットが吹き出していると考えられています。 こうしたジェットと外側の静止プラズマとの境界領域で、 ジェットの膨張に伴う希薄波が発生すると、 希薄波領域で新しいタイプの流体加速(異常加速)が起きることが Aloy & Rezzolla (2006) によって報告されました。一見不思議なこの現象は、相対論完全流体近似のもとで現れる断熱加速です。 Zenitani et al. (2010) はこの現象を磁気流体の相対論 HLLD シミュレーションで確認・検証し、 運動論的に見るとプラズマ熱速度の広がりに埋もれた バルク速度を見ていることを指摘しています。
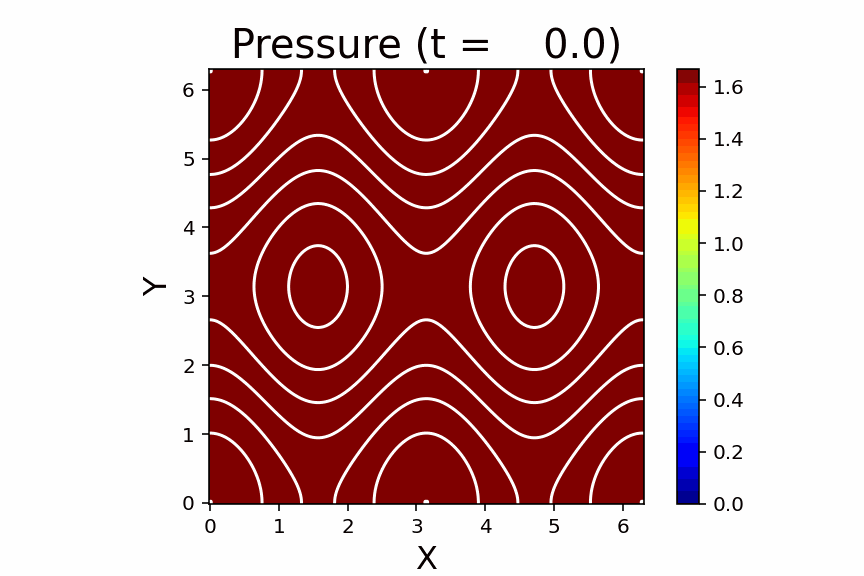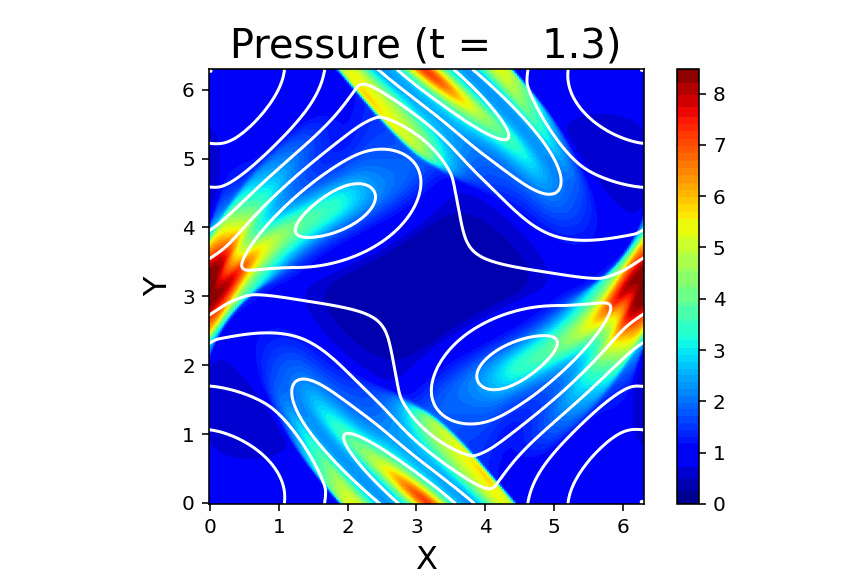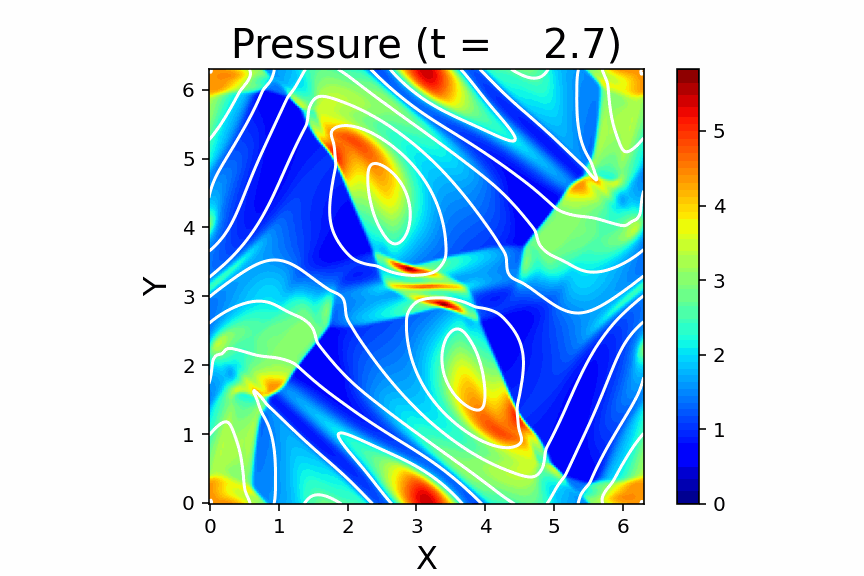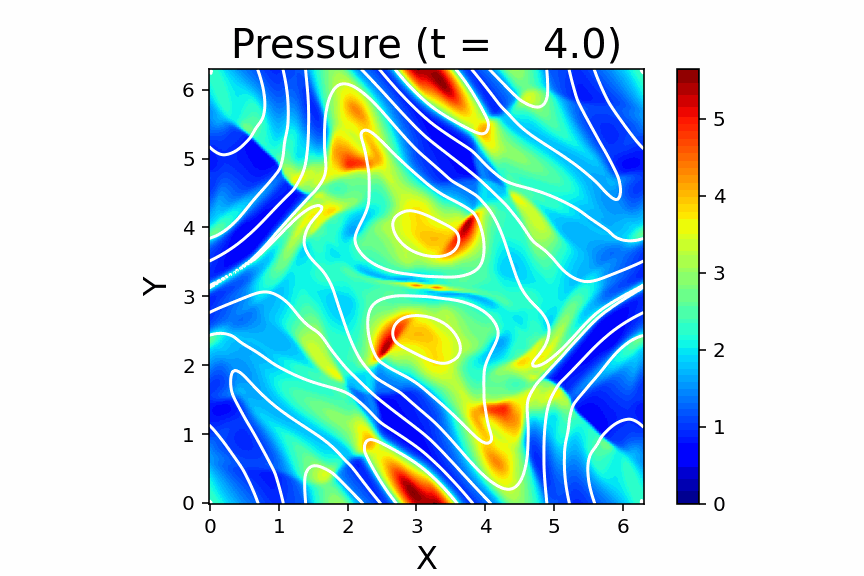
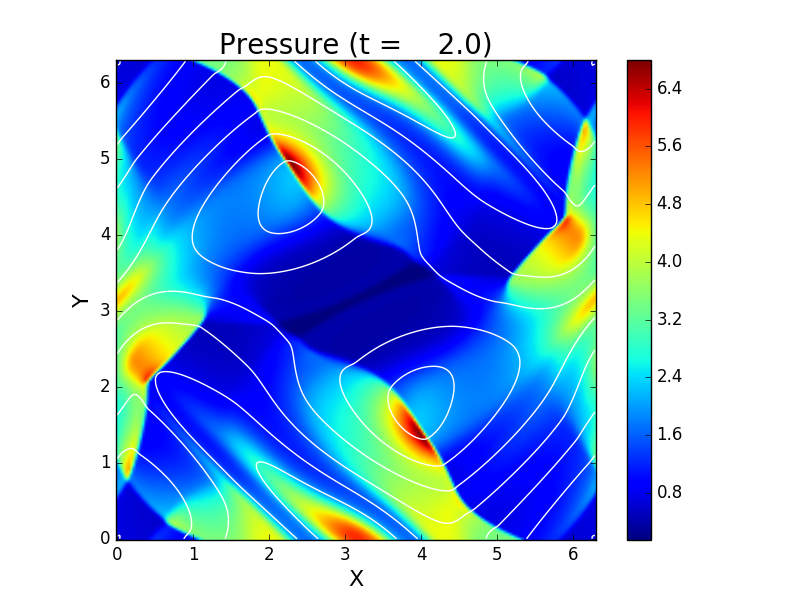
2次元渦問題
Orszag & Tang (1979) の渦問題を収録しています。渦が作り出した衝撃波が飛び交って複雑な模様を作り出すことや、磁場のソレノイダル性($\nabla\cdot\vec{B}=0$)が破れると計算が発散しやすいこともあり、2次元 MHD の標準問題として広く使われています。
磁場のソレノイダル問題の重要性を確認するために、
例えば main.f90 コードの102行目をコメントアウトして、
その後4箇所の flux_solver の引数 ch をゼロにしてみてください。
こうすると、ソレノイダル問題の補正項の働きがオフになって
非物理的な効果が累積するため、途中で計算が破綻します。
Kelvin-Helmoholtz 不安定
速度差がある2つの領域の境界層では、大きな渦が成長することが知られています。
これは Kelvin-Helmoholtz(KH)不安定 という流体力学の不安定です。
ここでは、Matsumoto & Hoshino (2004) に倣って、磁気流体での KH の渦の成長を見てみましょう。
初期条件ファイル(model.f90 )の中では、以下のような設定を用いています。
上下 (y) 方向には、上側が左向き、下側が右向きの速度勾配を tanh 関数で設定しています。
さらに、下側密度に相当するパラメーターαを使って、上下に密度差を入れています。
α=1 のとき密度は一様で、α=0.2 のとき上下に 5 倍の密度差ができます。
磁場は面に垂直な方向を向いています。
解像度は、最初に計算を試す場合は 160 [X] x 200 [Y] で十分でしょう。 その後、細かな構造を見る場合は 320 [X] x 400 [Y] 以上に解像度を上げていってください。 下図は、解像度 480 [X] x 600 [Y], α=0.2 の計算結果です。 巻き込んだ渦の境界面に、2次的な構造(K-H 不安定あるいは R-T 不安定)が出来ています。
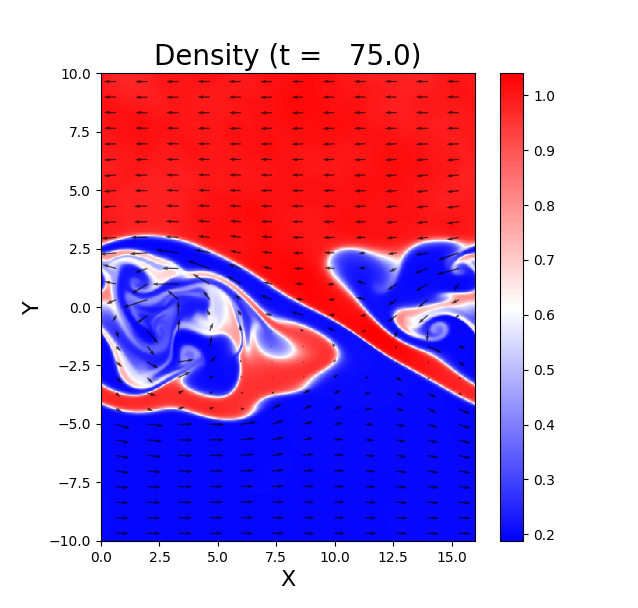
磁気流体中の KH 不安定は、磁場の向きと不安定の波数方向の関係によって、 成長の仕方が大きく変わります。例えば、初期条件に以下のように変えてみましょう。 面内にある磁場は張力を生じて、渦の上下方向の運動にブレーキをかけようとします。 渦の成長がどう変わるのか、計算して確かめてみましょう。
U(i,j,bx) = 0.d0
U(i,j,bz) = 0.d0
U(i,j,bx) = 0.2d0
U(i,j,bz) = 0.d0
この $B_x$ の値を大きく/小さくすると、磁場によるブレーキ効果も強く/弱くなります。 渦を止めるのに必要な $B_x$ の大きさは何で決まるでしょうか?
磁気リコネクション
宇宙空間プラズマ中で磁場が反転する電流層では、 磁力線が激しくつなぎ変わる「磁気リコネクション」が起きます。 磁気リコネクションは、理想 MHD 近似では起きませんが、 オームの法則に電気抵抗を取り入れた抵抗性 MHD 近似では扱うことができます。 OpenMHD には、Zenitani & Miyoshi (2011, 2015) で使った磁気リコネクションコードの後継版を収録しています。 初期条件は、以下のような磁場反転構造です。
\begin{align} \vec{B}(y) &= B_0 \tanh(y/L) {\hat{x}},\\ \vec{v} &= 0,\\ \rho(y) &= \rho_0 \big[ 1 + \cosh^{-2}(y/L)/ \beta_{\rm in} \big], \\ p(y) &= p_0 \big[ \beta_{\rm in} + \cosh^{-2}(y/L) \big], \end{align}この $\beta_{\rm in}$ は、プラズマベータ(磁気圧に対するプラズマ圧力の比)を上流のインフロー領域で評価したものです。簡単のため、系全体で温度($T=p/\rho$)を一定にしています。磁場が弱い真ん中(y ~ 0)付近では磁気圧が働かないため、代わりにプラズマの圧力を増やして全体構造を支えています。このような構造を「プラズマシート」あるいは「電流シート」と呼びます。この課題では (1) 原点付近の電気抵抗を強くしたうえで (2) 擾乱ポテンシャルを用いて 3% 程度の弱い磁場を追加して、リコネクションを起こしています。
\begin{align} \eta(x,y) &= \eta_0 + (\eta_1-\eta_0)\cosh^{-2} ( \sqrt{x^2+y^2} ) \\ \delta A_z &= 0.03 \times 2LB_0 \exp[-(x^2+y^2)/(2L)^2 ] \end{align}
いくつかファイルがあるうち、main.f90 がシリアルコード、mainp.f90 が並列コードです。系の対称性を利用して、第一象限のみを計算して全体の計算量を節約しています。
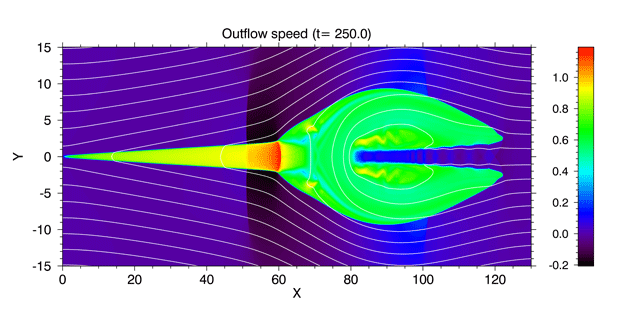
上の図は、デフォルトの設定で計算した磁気リコネクションの横方向の速度($V_x$)です。 リコネクション点からは高速のプラズマジェットが吹き出していて、その速度は簡単な議論から上流プラズマの Alfven 速度程度であることがわかっています。 ジェットの(音速に対する)マッハ数が1を超えた場合、下流側に複雑な衝撃波や不連続面を作ります。 こうした不連続面構造をまとめたものが、下の2016年版「プラズモイド・ダイアグラム」(解説記事)です。
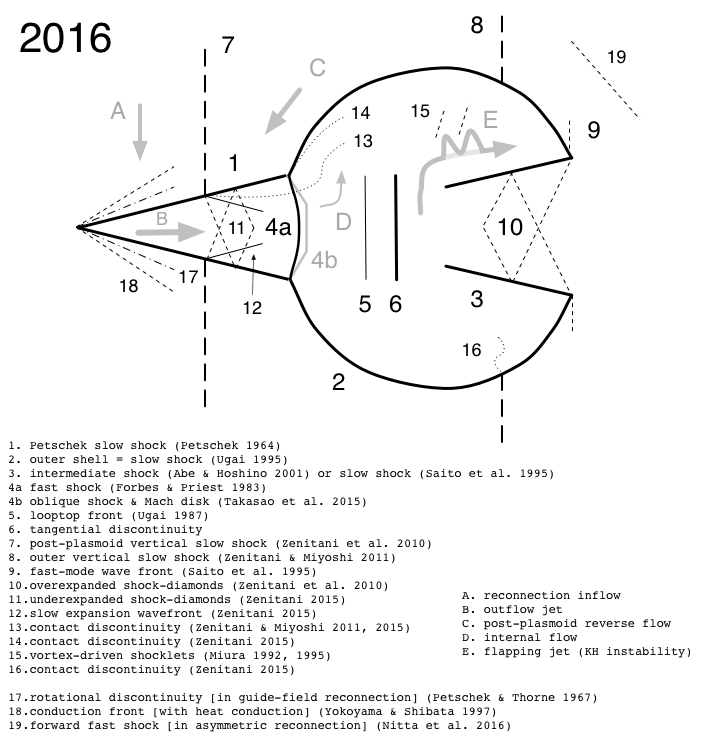
MHD リコネクションは半世紀以上も研究されていますが、 未解明の基本問題も多く残っており、 著者の腕次第で研究成果を出すことは可能です。 OpenMHD コードが皆様の研究をアシストできれば幸いです。
3次元磁気ループ移流問題
Gardiner & Stone (2008) で提案された、斜めの磁気ループを移流させるテスト問題です。 多次元でのコードの性能、特に接線不連続面(tangential discontinuity)の分解能力と安定性を 調べるためによく使われます。以下のような初期条件を用います。
\begin{align} \rho &= 1, \\ p &= 1, \\ \vec{v} &= (1,1,2) \\ A_3(r) &= 0.001 ~ {\rm max}( 0.3 - r, 0 ) \\ r &\equiv \sqrt{x^2_1+x_2^2} \end{align}A はベクトルポテンシャルで、添え字の 1,2,3 は斜めに傾いた系での座標を表しています。 磁場 B は $\vec{B} = \nabla \times \vec{A}$ から計算します。 詳細は原論文を参照してください。
この設定では、プラズマベータが高く磁場自体はほとんど圧力を持っていません。 磁場は全体の流れに乗って流されるだけになりますから、 元のループ構造が良く保たれるかどうかは数値解法の性能で決まります。 下の図は、一定時間後の磁気エネルギーの大きさの空間分布です。
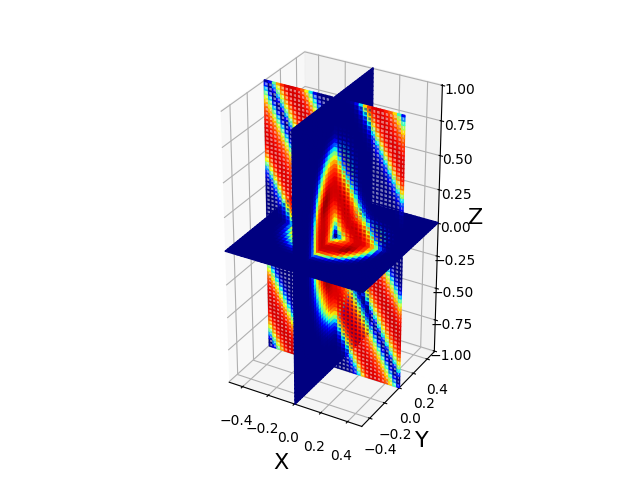
- 多次元の場合、計算セル(ボクセル)の各方向の長さの比率は?
簡単のため、Δx = Δy = Δz に固定しています。 比率を変えるためには、Runge=Kutta ソルバーやタイムステップ部分など、 何箇所かコードを修正する必要があります。
- OpenMHD で使っている単位系は?
Lorentz-Heaviside 系(Heaviside-Lorentz 系)を使っています。馴染みのない方は、東北工業大学 中川先生の解説を参考にしてください。$\mu_0$ や $4\pi$ などが含まれない Lorentz-Heaviside スタイルの表式を使っています。 MHD方程式には光速cが含まれないので、$c=1$となるLorentz-Heaviside単位系とは少し異なります。
- 現実世界のパラメーターに合わせるには?
速度(Alfven速度)・距離(典型スケール)・時間(典型時間)などを合わせると良いと思いますが、 数値計算上の都合で、例えばプラズマβや電気抵抗には人工的な値を入れざるを得ません。 さまざまな制約下での計算結果を使って現実を推測するところが、シミュレーション研究の腕の見せ所です。
-
IDLのプロット画面が真っ黒で何も表示されない
X ウィンドウをリモートで表示すると、 OpenGL のハードウェア加速機能が効かないために 画面が真っ黒になってしまうことがあります。 この場合は、IDL をソフトウェアレンダリングモードで動作させる必要があります。
IDLを起動するときに、以下のオプションを追加するか、
$ idl -IDL_GR_X_RENDERER 1
あるいは、IDL の
image関数にrenderer=1というオプションを追加すると良いでしょう。 このオプションは、付属プログラムのコメント部分に記述しています。;; 2D image myimg = image(data[*,*,vx],x,y,axis_style=2,xtitle='$X$',ytitle='$Y$',xtickdir=1,xticklen=0.02,ytickdir=1,yticklen=0.01,font_size=16,rgb_table=13,dimensions=[1000,500]) ;; ,renderer=1) ;; use software rendering over a remote connection.
-
Linux 版 IDL で libXp.so.6 が見つからない、というエラーが出る。
Ubuntu Linux であれば、以下のライブラリを追加インストールしてください。 CentOS の場合は、西田さんのメモが参考になると思います。
sudo apt install libxp6
- macOS 版 IDL で "Error: attempt to add non-widget child "dsm" to parent "idl" which supports only widgets" というエラーのため、ウィンドウが表示されない。
- Jupyter ノートブックで表示されるグラフを大きくしたい。
ノートブックの先頭付近に以下の行を追加して グラフのデフォルトサイズを変更することができます。 (横、縦)をインチ数で指定します。 この plt は matplotlib.pyplot のインポート名です。
plt.rcParams['figure.figsize'] = (6.4, 4.8)
- Python のプロットのカラーマップ一覧を知りたい
Matplotlib 公式サイトにカラーマップ一覧があります。
- 並列版のデータ形式は?
シリアル版と同様、1つのファイルにデータを書き出します。
ファイル先頭付近の変数を
io_type = 0に変更すると、 並列プロセス毎にファイルを書き出します。 自作プログラムでデータを加工する場合は、 各ファイルに1グリッドずつののりしろが含まれていることを考慮してください。 - 計算結果を 〜のように解析したい
ぜひ自分の手でプログラミングしてみてください。 PythonもIDLも汎用言語ですから、思いのままの解析ができるはずです。
- のりしろは1グリッドで足りるのでしょうか?
はい。のりしろデータをノード間で転送したあと、 MUSCL補間した基本量をさらにノード間転送しています。 この過程で2グリッド先の情報が伝わっています。
-
初期設定はどこで設定していますか?
以下の箇所です。
- メインファイル(
main.f90, mainp.f90, main.cuf, mainp.cuf) --- グリッド数、並列数、数値解法の選択などを計算全体の設定を定義しています。 - モデル設定ファイル(
model.f90, modelp.f90) --- 空間座標や物理量の値を定義しています。 以下の変数で、X方向の始点・終点と、Y方向の始点の位置を指定します。 Y方向の終点はグリッド数から自動計算されます。! x & y positions (Note: domain_y(2) is automatically calculated) real(8), parameter :: domain_x(2) = (/0.d0, 200.d0/) real(8), parameter :: domain_y(1) = (/0.d0/)
また、磁気リコネクション問題の電気抵抗 $\eta$ は resistive flux ルーチン(
flux_resistive.f90)で 定義しています。-
eta関数:電気抵抗の関数形を定義しています。 -
set_dt_resistiveルーチン:時間ステップを制限します。
- メインファイル(
- 境界条件を設定するには?
シリアル版では
bc*.f90、並列版ではmpibc*.f90で 境界条件を設定しています。-
(mpi)bc_for_Uルーチン --- 保存量(U)の境界条件を設定します。 -
(mpi)bc_for_Fルーチン --- X方向にMUSCL補間した基本量(VL, VR)の境界条件を設定します。 これをX方向の数値流束 F の計算に利用します。 -
(mpi)bc_for_Gルーチン --- Y方向にMUSCL補間した基本量(VL, VR)の境界条件を設定します。 これをY方向の数値流束 G の計算に利用します。 -
(mpi)bc_for_Hルーチン --- Z方向にMUSCL補間した基本量(VL, VR)の境界条件を設定します。 これをZ方向の数値流束 H の計算に利用します。
並列版では、メインファイル(
mainp.f90, mainp.cuf)先頭付近のbc_periodicity変数を、 周期境界では.true.、そうでない場合は.false.にセットして下さい。 以下は、X方向を周期境界、Y方向を別の境界条件を利用する例です。 これを.true.にした場合、その方向の周期境界の処理は通信モジュールが行います。 境界条件ファイル(mpibc.f90)のmpibc_for_U, mpibc_for_F, mpibc_for_Gの中で 同じ処理を書く必要はありません。logical, parameter :: bc_periodicity(2) = (/.true., .false./)
仮想ポテンシャル $\psi$ の境界条件は特に注意してください。 値の小さな補正項なので符号を間違えても動いてしまいますが、 エラーを累積した後で結果を変えるので厄介です。
-
- 一番開発が大変だった箇所は?
並列通信モジュール(
parallel.f90)です。 -
MPI-3 の共有メモリ通信を使うには?
並列通信モジュール(
parallel.f90)の以下の箇所をuse_shm = .true.に変更すると、 ノード内通信を共有メモリのデータコピーで代用します。 これは実験的な機能です。! ----- MPI-3 shared memory communication ------------------------ logical, parameter, private :: use_shm = .false. ! MPI communication ! logical, parameter, private :: use_shm = .true. ! MPI-3 SHM model (experimental)
-
MUSCL補間は、特性変数に対して行った方が良いのではないでしょうか?
はい、波に乗って運ばれるのは特性変数ですから、 特性変数を補間した方が良いでしょう。 しかし、物理量を特性変数に変換する計算コストがかなり大きいため、 OpenMHDでは基本変数の補間で代用しています。 2次精度では特性変数 vs 基本量の違いはあまり気にならないと思います。
なるべく計算を軽くし、代わりにグリッド数を増やして 実質精度を上げることを目指しています。
- お薦めの補間方法はどれでしょうか?
デフォルトでは最も無難な minmod リミターを採用しています。 minmod, van Leer, MC, Koren のうち、 下線 のものを条件文(if 文)を使わずに実装しています。
-
HLLD ソルバーの中に HLLC ソルバーが入っているのはなぜでしょうか?
HLLD 法は、リーマンファンの中に Alfven speed で広がる回転不連続面(RD)を考え、 さらにその外側に fast speed で広がる外側境界を考えます。 低ベータ(β≦1.2)プラズマでは、 教科書やこちらのプロットで確認できるように、 磁力線方向の Alfven speed は fast speed とほぼ同じです。 そのため沿磁力線方向では、片方の RD が外側境界を追い越してしまって、 HLLD 法の4状態の仮定が成立しなくなることが稀にあります。 これは、HLLD 論文 [1] の p.326 冒頭で言及されている 0/0 問題に関係しています。
OpenMHD は、RD と外側境界が接近して HLLD 法の仮定が破れそうになると、 RD を取り払って HLLC 法にスイッチします。
-
HLLD 法はガリレイ変換に対して不変なのでしょうか?
HLLD ソルバーは非線形ソルバーなので、ガリレイ不変ではありません。
-
圧力p や密度ρをゼロにできますか?
できません。計算が止まります。
-
保存量配列 U や基本量配列 V の最後の引数は、ただの整数では?
はい。例えば
U(i,j,en)とU(i,j,4)は全く同じです。 このenは、コードを読みやすくするために使っている定数で param.h ファイルで定義しています。 -
多次元データの最後の成分(ps)は何ですか?
磁場の発散部分($\nabla \cdot \vec{B}$)に溜まる数値誤差を 拡散・減衰させるための仮想ポテンシャル($\psi$: psi)です。 物理的な意味はありません。 (「はじめに > 基礎方程式と計算手法」参照)
-
計算時間はどのくらいかかるのでしょうか?
デフォルトのリコネクション問題(
2D_reconnection/mainp.f90)では、 Intelコンパイラ(ifort)でコンパイルしたプログラムを ブーストクロック 5.0 [GHz] の Intel i9 プロセッサ4並列(4コア)で走らせると、 23分(HLL)〜28分(HLLD)かかりました。 他の CPU/GPU での計測結果は以下のとおりです。 2次元シミュレーションの計算コストは解像度の3乗に比例しますから、 PCやGPUの性能に応じて計算サイズと解像度を調整すれば良いでしょう。Intel i9-9900K プロセッサ・MPI 4並列 28分 AMD EPYC 7742 プロセッサ・MPI 4並列 24分50秒 AMD EPYC 7742 プロセッサ・MPI 64並列 1分50秒 Apple M4 プロセッサ・MPI 4並列 12分40秒 NVIDIA Tesla T4 GPU (Google Colab) 5分 NVIDIA GeForce RTX 2080 GPU 2分10秒 NVIDIA RTX A6000 GPU 1分50秒 NVIDIA GV100 GPU 1分20秒 NVIDIA A100 GPU 35秒 -
論文を引用したい
HLLDコードをお使いの場合は、文献 [1] と、GitHub の URL (https://github.com/zenitani/OpenMHD) あるいは Astrophysics Source Code Library のエントリー番号 (ascl:1604.001) を紹介してくださると嬉しいです。 ドキュメントの多くを [1] の一環で整備していますが、[1] にはコードの入手先(特にURL)の情報がありません。 そこで、別途、GitHub or ASCL の情報を追加してくださると、 読者がこのページに到達することができるようになります。 文例を以下に示します。 GitHub の場合は、本文中に URL があるだけでも良いと思います。
Physics of Plasmas スタイルの文例:
S. Zenitani, Phys. Plasmas, 22, 032114 (2015). S. Zenitani, Astrophysics Source Code Library, record ascl:1604.001 (2016).
ApJ スタイルの文例:
Zenitani, S. 2015, PhPl, 22, 032114 Zenitani, S. 2016, OpenMHD: Godunov-type code for ideal/resistive magnetohydrodynamics, Astrophysics Source Code Library, ascl:1604.001
-
URLを紹介したい
このページの URL (https://sci.nao.ac.jp/MEMBER/zenitani/openmhd-j.html) は 作者の異動やサーバー環境の都合で変わる可能性があります。 変更の可能性が少ない GitHub (https://github.com/zenitani/OpenMHD) あるいは Astrophysics Source Code Library (ASCL) (https://ascl.net/1604.001) の URL を紹介してくださればと思います。
-
CFL数を小さめ(0.5以下)に設定しているのはなぜでしょうか?
作者の好みです。Δt/Δx > 0.5 に設定すると、 両側のセル境界からやってきた波が真ん中でぶつかり、直感に合わないと思うのです。 Toth (2010) の教科書の pp.216--218 によると Δt/Δx<1.0 で良いそうですが、私はどうも納得がいきません。
-
計算を途中からリスタートするには?
一部のコードには、メインファイル先頭近くに
n_startという変数があります。 この変数を0にすると計算を最初から実行、1以上にすると1番目のデータファイルを読み込んで計算を再開、-1にするとファイル番号を予想して計算を再開します。! If non-zero, restart from a previous file. If negative, find a restart file backword in time. integer :: n_start = 0
-
計算コストがかかるのはどこの部分でしょうか?
HLLD フラックスの部分です。 (ベンチマーク結果)
-
MPI 並列計算が思ったほど速くない。
後述の OpenMP 並列が思いがけず有効になっていることがあります。 コンパイラのオプションをよく確認してください。
-
OpenMP を使うには?
Makefile のコンパイラ引数に Intel fortran では
-qopenmp、 gfortran では-fopenmpオプションを追加してください。そして、プログラムを実行する際に、環境変数
OMP_NUM_THREADSを使って並列スレッド数を設定します。$ export OMP_NUM_THREADS=4 $ ./a.out
全体の環境変数を変えたくなければ、以下でも良いでしょう。
$ OMP_NUM_THREADS=4 ./a.out
これに関連して、Cray fortran でフラット MPI を使う場合、 ユーザーの意図に反して OpenMP がオンになってしまうことがあります。 その場合は、Makefile でコンパイラに
-hnoompオプションを渡して OpenMP を明示的にオフにしてください。F90 = ftn -hnoomp
-
OpenMP を使うと、
segmentation fault...でプログラムが異常終了する。以下のどちらかのコマンドを使って、 シェルのスタックサイズの制限を解除してください。
$ ulimit -s unlimited % unlimit stacksize
Intel Fortran では
-heap-arraysオプションを 使うことができるそうです。 -
スーパーコンピューターで実行した計算が途中で止まった?
ログファイルを参考にしてください。 スーパーコンピューターで計算ジョブが実行されると、 プログラムの出力とエラー出力を記録したログファイル(テキストファイル)が、 それぞれ、同じディレクトリ内に生成されます。 ファイル名はスパコンによって違います。
-
ベンチマークの計測方法は?
UNIX の time コマンド を使っています。 並列計算では、CPU 時間に含まれない ネットワークの遅延時間がかかりますので、 全てを含めた real タイムを見てください。 MPI 並列と OpenMP 並列を併用する場合、 最適のノード数・スレッド数はケース・バイ・ケースで変わりますから、 自分で検証してみてください。
$ time ./a.out $ time mpirun -np 16 ./ap.out $ OMP_NUM_THREADS=16 time ./a.out
-
国立天文台のスーパーコンピューター(xc50)でコードを動かすには?
Cray コンパイラでMPIを使う場合は、 以下のように
-hnoompオプションを追加します。F90 = ftn -hnoomp
例えば、お試し用の XC-trial カテゴリで 120 コアを使う場合は、 次のようなジョブスクリプト(
test.sh)を用意します。#PBS -N jobname #PBS -l nodes=3 # 使用ノード数 #PBS -j oe #PBS -q large-t cd ${PBS_O_WORKDIR} aprun -n 120 -N 40 ./ap.out > output.log # end
そして、qsubコマンドとジョブスクリプト(
test.sh)を使って ジョブを投入してください。$ qsub test.sh
-
UNIX操作に不慣れなのですが...
WikiBookや UNIX 標準テキスト、 UNIX/Linux の基礎知識(京大) などを参考にして、少しずつ慣れていってください。
-
リモートサーバーにログインするには?
Linux, macOS のターミナル、Windows 10(バージョン1803以降)のPowerShellで ssh コマンド を使ってください。
-
リモートサーバーとファイルをやりとりするには?
Linux, macOS, Windows 10(バージョン1803以降)では
scpコマンドを使うことができます。 Linux, macOS ではrsyncコマンドを使うこともできます。 macOS の Fetch(学生・教育関係者は無料)、Windows の WinSCP、 Linux/macOS/WindowsのFileZillaなど、GUIの sftp クライアントソフトも便利です。 -
Fortran 90, Python, IDL コードをシンタックスハイライト(文法カラーリング)できるテキストエディタは?
Emacs, Vim, Smultron なら全ての言語に対応しています。Visual Studio Code (VS Code) は Python extension に加えて、Marketplaceで Modern Fortran および IDL: Interactive Data Language 対応モジュールを追加することができます。macOS では BBEdit と CotEditor が Fortran 90, Python に対応しています。
-
計算中の画面のまま、ログアウトしたい(UNIX 中級者向け)
screen コマンド を使うと、 途中画面を出力したままログアウト(デタッチ)して、後で再び接続(アタッチ)することができます。 screenは、デフォルトでは少し使いにくいので、以下のサイトを参考にカスタマイズしても良いと思います。 screenの設定は
.screenrcファイルを編集して行います。
-
Open MPI, OpenMP, OpenMHD って紛らわしくないですか?
Gravity wave と gravitational wave と同じぐらい紛らわしいのは承知しています。 最後まで目を通してくださり、ありがとうございます。
Linux
gfortran + MPI のインストール
Ubuntu / Debian では、以下のような apt コマンドで fortran コンパイラ(gfortran)やMPIライブラリ(Open MPI, MPICH)を インストールすることができます。
$ sudo apt install gfortran $ sudo apt install openmpi-bin libopenmpi-dev # MPIライブラリに Open MPI を使う場合 $ sudo apt install mpich libmpich-dev # MPICH を使う場合
とします。
CentOS / RedHat をお使いの方は、代わりに yum を使います。 gfortran や MPI も以下の手順でインストールできます。
# yum install gcc-gfortran # yum install openmpi openmpi-devel # MPIライブラリに Open MPI を使う場合 # yum install mpich mpich-devel # MPICH を使う場合
また、これらの Ubuntu(CentOS も?)標準の方法では、 gfortran, gcc にバインドされたMPIライブラリがインストールされます。 例えば Intel fortran など、別のコンパイラにバインドする場合は、 後述の「MPIライブラリのインストール」を参考に自力でMPIライブラリをインストールしてください。
Intel HPC Toolkit + Intel MPI 環境のインストール
Intel の Web サイト から、 Intel oneAPI Base Toolkit と HPC Toolkit をダウンロードしてインストールします。
そして、ターミナルで setvars.sh スクリプトを走らせれば、
コンパイラ(ifort)や並列コンパイラ(mpiifort)を使う準備が整います。
$ . /opt/intel/oneapi/setvars.sh :: initializing oneAPI environment ... bash: BASH_VERSION = 5.2.21(1)-release args: Using "$@" for setvars.sh arguments: :: advisor -- latest ... :: oneAPI environment initialized ::
NVIDIA HPC SDK のインストール
NVIDIA の Web サイト から、 NVIDIA HPC SDK をダウンロードしてインストールします。
$ tar xpzf nvhpc_2026_261_Linux_x86_64_cuda_13.1.tar.gz $ cd nvhpc_2026_261_Linux_x86_64_cuda_13.1/ $ sudo ./install
そのうえで、/opt/nvidia/hpc_sdk/Linux_x86_64/2026/compilers/bin, /usr/local/cuda/bin
などに PATH を通せば良いでしょう。これで、コンパイラ(nvfortran)を使う準備が整います。
$ nvfortran -V nvfortran 26.1-0 64-bit target on x86-64 Linux -tp znver3 NVIDIA Compilers and Tools Copyright (c) 2026, NVIDIA CORPORATION & AFFILIATES. All rights reserved.
Python3 環境のインストール
最近の Linux には Python 3 系が 最初からインストールされています。 これに加えて matplotlib, ipython3 などをインストールすれば良いと思います。 Ubuntu / Debian では、以下のように apt コマンドを使えば良いようです。
$ sudo apt install python3-dev python3-matplotlib ipython3
また、日本 Python ユーザー会による 環境構築ガイドも 参考になると思います。
Windows
Windows Subsystem for Linux をインストールすると、Linux 環境を作ることができます。Linux で OpenMHD が動作します。
未確認情報ですが、CUDA on WSL 2 と NVIDIA HPC SDK を使うと、GPU計算もできるかもしれません。
macOS
Xcode のインストール
XCode は Apple 純正の開発環境で、 C コンパイラや make などの開発ツールが一通り入っています。 OS 付属のディスクあるいは AppStore からダウンロードして インストールしてください。 XCode 付属の C コンパイラや XCode がインストールするライブラリのバージョンが古いと、 gfortran を使ったプログラムのコンパイル・実行に影響が出ることがあります。 既に XCode をインストールしている方も、 いちどバージョンを確認して、なるべく最新版のものをインストールして下さい。 (例えば本稿執筆時点の XCode の最新バージョンは 26.2 です。)
XCode をインストール後、開発のためのコマンドラインツール(command line tools)を追加インストールする必要があります。次のコマンドを試してみてください。
$ xcode-select --install
コマンドラインツールのインストールが始まりますので、 ダイアログの指示に従ってください。 以下のようなメッセージが出る場合は、 既にコマンドラインツールがインストールされていますので それ以上の操作は必要ありません。
xcode-select: error: command line tools are already installed, use "Software Update" to install updates
gfortran のインストール
gfortran は、Homebrew や MacPorts といった UNIX パッケージ集でインストールすることができます。 gfortran を単体でインストールするには、 以下のどちらかのサイトからファイルを入手することをお勧めします。
- Binaries available for gfortran -- GCC の準公式サイト。macOS 標準のインストーラーパッケージを配布しています。
- High Performance Computing for Mac OS X -- 長年、コンパイラのバイナリファイルを配布してくださっているサイト。ここから gfortran のバイナリをダウンロードできます。
最近の macOS では、前者のパッケージを使うほうが無難だと思います。 後者を使う場合は、アーカイブファイルを以下のように手動で展開します。
$ sudo tar xvf ~/Downloads/gfortran-14.1-m1-bin.tar.gz -C /
gfortran でプロダクト・ラン(本計算)を走らせる場合は、
必ず -O2 以上の最適化オプションを使うようにしてください。
このオプションをオンにすることで、市販のコンパイラと同程度まで
プログラムが速く動作するようになります。
また、gfortran は OpenMP に対応しています。
2〜8 程度のコア数であれば、後述の Open MPI をインストールしなくても
並列計算を行うことができます。
OpenMP を使う場合は、Q & A でも説明しているように
コンパイラオプション -fopenmp を使ってください。
Python3 + matplotlib のインストール
OpenMHD では可視化に Python 3 + matplotlib を用います。 macOSのデフォルトのpythonはバージョンが古いことが多いので、 Homebrew や MacPorts といった UNIX パッケージ集、あるいは Anaconda などのディストリビューションを使って、 Pythonや周辺ライブラリをインストールした方が良いでしょう。
ここではPython公式サイトのパッケージを使う方法を紹介します。 以下のサイトから Python パッケージをダウンロードしてインストールしてください。
- Python.org --「Download」タブからファイルをダウンロードできます。
次にPython標準のパッケージ管理システム pip コマンドを使って
Python のライブラリをインストールしていきます。
例えば matplotlib をインストールしてみましょう。
$ pip3 install matplotlib
システムによっては、コマンド名は pip かもしれません。
適宜、pip3 を pip と読み替えてください。
さらに追加して、IPython という高機能シェルをインストールすることをお勧めします。 IPython では、タブキーによる変数・ファイル名補完などが効きますので、 便利に作業できるようになります。
$ pip3 install ipython
可視化に Jupyter, Pillow, OpenCV を使う場合は、 pip でインストールしてください。
$ pip3 install jupyter $ pip3 install pillow opencv-python
インストール済みのライブラリをアップデートする場合は、 -U オプションを使います。
$ pip3 install -U matplotlib
以下のように IPython シェルを立ち上げてみましょう。 matplotlib がインストールできているかどうか、確認してみてください。 最後に exit で終了しています。
$ ipython3 --pylab Python 3.14.3 (v3.14.3:323c59a5e34, Feb 3 2026, 11:41:37) [Clang 16.0.0 (clang-1600.0.26.6)] Type 'copyright', 'credits' or 'license' for more information Using matplotlib backend: macosx In [1]: print(matplotlib.__version__) 3.10.8 In [2]: exit
Linux, macOS 共通
MPIライブラリのインストール
コア数の多いスーパーコンピューターでは、 MPI並列(フラット MPI)、あるいは MPI と OpenMP を併用したハイブリッド並列が有効です。 PC・ワークステーションにもMPIライブラリをインストールすれば、 スパコンと同じ並列条件でプログラムを開発・実行することができます。 MPIライブラリは、使用するコンパイラにあわせてインストールする必要があります。 そこで、以下のサイトからMPIライブラリのソースコードをダウンロードして、 自分でコンパイル&インストールすることをお勧めします。
ここでは、gfortran用の Open MPI を /opt/openmpi64g、
Intel fortran 用の Open MPI を /opt/openmpi64i... のように
それぞれ別のディレクトリにインストールすることを考えます。
コンパイラが1種類だけであれば、以下のコマンド例の
--prefix= オプションを指定しなくても結構です。
その場合は、/usr/local にファイルがインストールされます。
/opt/openmpi5 ディレクトリに
gfortran用の Open MPI をインストールするには以下のようにします。
configure と make には時間がかかりますが、気長に待ってください。
make は並列コンパイルに対応しています。
作業を早く終わらせたい場合は、-j オプションを使ってください。
$ tar jxvf openmpi-5.0.9.tar.bz2 $ cd openmpi-5.0.9 $ ./configure --prefix=/opt/openmpi5 $ make [ $ make -j 8 ] $ sudo make install
以下は、/opt/mpich5 ディレクトリに MPICH をインストールした手順です。
必要に応じて ./configure --prefix=/opt/mpich5 FC=__my_compiler__ のようにして
FC オプションでコンパイラ名を調整してください。
$ tar zxvf mpich-5.0.0.tar.gz $ cd mpich-5.0.0 $ ./configure --prefix=/opt/mpich5 $ make [ $ make -j 8 ] $ sudo make install
最後に、mpirunコマンドを実行して、 MPIライブラリのバージョン情報を確認してください。
$ /opt/openmpi5/bin/mpirun --version mpirun (Open MPI) 5.0.9 Report bugs to https://www.open-mpi.org/community/help/
$ /opt/mpich5/bin/mpirun --version
HYDRA build details:
Version: 5.0.0
Release Date: Tue Feb 3 16:42:12 CST 2026
- To Do
2026-XX-YY - CPU版の通信モジュールで、Haloデータをバッファを経由せず直接送受信するようにしました。
- 2025-08-04
- LLF法の磁場のフラックス計算にバグがありました。(Kiwan Parkさんに感謝)
flux_type=4でLHLLD法(圧力補正項)の試験実装に切り替わります。
- 2024-11-24
- 3次元磁気ループ問題と3次元磁気リコネクション問題(GPU版のみ)を収録しました。
- 収録課題の一部(太陽風共回転領域問題と3次元Orszag-Tang渦問題)を配布物から外しました。
- 磁気リコネクション問題の電気抵抗の設定方法を変更しました。
- サポートドキュメントをアップデートしました。
- 2024-01-30
- 3次元Orszag-Tang渦問題を収録しました。
- Intelコンパイラの移行に備えて、コンパイルコマンド名を
ifort, mpiifortからifx, mpiifort -fc=ifcに変更しました。 - ディレクトリ構成を少し変更。
- 2023-08-03
- GPU版Makefileのnvfortranコンパイラのオプションを変更。
- 2023-02-18
- HLLDソルバーのOpenMP並列化時の問題を改善しました。
- MakefileにAMDコンパイラ(AOCC)のコマンド例を追加。
- ウェブページの記述を増やしました。
- 2022-05-01
- 一様電気抵抗用の流束ソルバー(
flux_resistive_uni)を追加しました。 - その他、多くのマイナー変更。
- 一様電気抵抗用の流束ソルバー(
- 2021-08-01
- Hyperbolic div cleaning 用の流束ソルバー(
flux_glm)をHLLDソルバー(flux_solver)に統合しました。 - 途中データからリスタートする時、前のデータファイルを上書きしないようにしました。
- GPU版のメモリ使用量を削減しました。
- GPU-MPI版の通信モジュールに問題がありました。このバージョンで修正しました。
- Python/IDL データ読み込みルーチン(
data_read)にxrange, yrangeキーワードを追加しました。
- Hyperbolic div cleaning 用の流束ソルバー(
- 2020-11-01
- 2020-08-30版 CPUコードの電気抵抗計算部(
flux_resistive)に重大なミスがありました。(名下宥佑さんに感謝) - 磁気リコネクション問題の境界条件を修正しました。ガイド磁場リコネクションで軽微な影響が出ていた可能性。
- 2020-08-30版 CPUコードの電気抵抗計算部(
- 2020-08-30
- GPU版、GPU-MPI版を収録しました。(近藤光志さんのテスト協力に感謝)
- 一部のルーチン(
glm_ss2, flux_resistive)の引数を変更。 - リコネクション問題のファイルを整理しました。
- 2019-12-27
- コメント・ドキュメントの微修正。
- 2019-05-01
- 全物理課題に可視化用 Jupyter ノートブックを追加しました。
ipywidgetsによるインタラクティブ操作にも対応。(和田智秀さんに感謝) - ムービー作成用のサンプルスクリプトを追加しました。(河村聡人さん、坪内健さんに感謝)
- Python, IDL のデータ読み込みルーチン
data_readで、ファイル番号に加えてファイル名を指定できるようにしました。
- 全物理課題に可視化用 Jupyter ノートブックを追加しました。
- 2019-01-25
- 途中データからのリスタート方法を変更しました。
n_start< 0 のとき、ファイルを自動検索します。
- 途中データからのリスタート方法を変更しました。
- 2018-05-10
- MPI-3 に移行しました。
- 計算領域を多次元分割するようにしました。
- ノード内通信に MPI-3 shared memory モデル(Hoefler et al. 2013)を選択可能に。
- ファイル構成を整理しました。
- 2018-03-14
- OpenMP によるスレッド並列性能を改良しました。
- 2018-02-14
- MPI 通信にノンブロッキング通信を採用。
- 並列 I/O の動作を修正しました。
- OpenMP 利用時における HLLD ソルバーのバグを修正しました。
- その他、多くの微修正。
- 2017-07-28
- 相対論ジェットの境界層問題を収録しました。
- 相対論 HLL/HLLD コード(垂直伝搬専用)を収録。基本量を v から u に変更。
- Python/IDL 可視化ルーチンを改良。
- 2017-04-28
- データのファイル形式を変更しました。こちらを参考に fortran の record_marker を使わないようにしました。(近藤光志さん、堀田英之さん、松本倫明さんに感謝)
- 収録課題の解説をひととおり用意しました。
- Python/IDL 可視化ルーチンを改良。
- Mathematica のサンプルノートブックを一時的に削除。
- 2016-12-26
- Python/IDL 可視化ルーチンを改良。
- Mathematica のサンプルノートブックを追加。
- 2016-10-08
- Slope limiter を統合し、OpenMP ディレクティブを追加。
- Flux ソルバーを統合・高速化。
- Resistive 項と GLM 項の扱いを変更。
- 全体的な性能向上。
- HLLC ソルバー(x方向)のエネルギー評価のバグを修正。
- 初期設定の微調整。(日野太陽さんに感謝)
- Python 3 (matplotlib) の可視化ルーチンを収録。
- ディレクトリ名をわかりやすく変更。
- ウェブページの解説を増やしました。
- 2016-08-08
- 磁気リコネクション問題の初期条件・境界条件を微調整。(近藤光志さんに感謝)
- IDL 可視化ルーチンを収録。
- gnuplot の可視化サンプルコードを収録。(和田智秀さんに感謝)
- 2016-01-17
- HLLC ソルバーと Koren リミターを高速化。
- Flux ソルバーに OpenMP ディレクティブを追加。
- 2015-08-15
- 並列 I/O に対応。
- Resistive HLL ソルバーの電流の計算方法を変更。
- LLF/HLL/HLLC ソルバーと minmod/MC リミターを、特にSPARC機で高速化。
HLLC ソルバー(x方向)のエネルギー評価のバグを修正。
- 2015-03-25
- 磁気リコネクション問題の新しい設定(文献 [2])を収録。
- 一部の境界処理のファイル名を変更。
- コード全体の高速化。
- 2014-09-08
- Resistive HLLD ソルバーを追加。
- 途中データからリスタートできるようになりました。
- 特殊な状況で fast-mode 速度が NaN になる問題に対処。
- GitHub に公開リポジトリを設置。
- 2012-07-05
- CIR 問題を収録。
- Koren リミターを追加。
- 2011-01-12
- 磁気リコネクション問題(文献 [1])および KH 不安定問題を収録。
- Resistive HLL ソルバーを追加。
- MPI による並列化。
- GLM 項の計算方法を変更。
- 2010-09-20
- OpenMHD コードと命名して公開。
- Hyperbolic divergence cleaning を実装。
- 2010-05-14
- HLLC-G/HLLD ソルバーのプロトタイプを実装。
- 1次元及び2次元テスト問題。
相談先
OpenMHD コードのノウハウを共有したり、諸々の問題を解決するための メーリングリストを設けています。 良かったらこちらに問い合わせてみてください。
- OpenMHD ユーザーズグループ(参加者39名)
また、作者宛に直接、メールをいただいても結構です。 サポート・相談の必要度合いによっては、共同研究という形で進めた方が良い場合もあります。 その場合は、共同研究を申し込んでくだされば幸いです。
研究論文
2026年2月時点では、国内外の利用者グループから 以下の研究論文(査読付き)が出版されています。
- S. Zenitani & T. Miyoshi, Phys. Plasmas 18, 022105 (2011)
- S. Zenitani, Phys. Plasmas 22, 032114 (2015)
- S. Nitta, T. Wada, T. Fuchida, & K. Kondoh, Astrophys. J. 828, 63 (2016)
- T. Shimizu, K. Kondoh, & S. Zenitani, Physics of Plasmas 24, 112117 (2017)
- M. Hosseinpour, Y. Chen, & S. Zenitani, Physics of Plasmas 25, 102117 (2018)
- S. Nitta & K. Kondoh, Astrophys. J. 872, 147 (2019)
- W.-L. Teh & S. Zenitani, Astrophys. J. 885, 22 (2019)
- W.-L. Teh & S. Zenitani, Astrophys. J. 890, 114 (2020)
- S. Zenitani & T. Miyoshi, Astrophys. J. Lett. 894, L7 (2020)
- S. Nitta & K. Kondoh, Astrophys. J. 907, 21 (2021)
- W.-L. Teh & S. Zenitani, Earth and Space Science 8, e2020EA001449 (2021)
- H. Lofti & M. Hosseinpour, Front. Astron. Space Sci. 8, 768965 (2021)
- S. Nitta & K. Kondoh, Astrophys. J. 936, 125 (2022)
- S. Nayak, S. Sau, & S. Sanyal, Astropart. Phys. 146, 102805 (2023)
- M. Sarkhosh, M. Hosseinpour, &, M. A. Mohammadi, Braz. J. Phys. 54, 97 (2024)
- H. Lofti, J. Theor. Appl. Phys. 18, 1 (2024)
- D. Bisht, D. Kumar, S. Nayak, & S. Sanyal, Int. J. Mod. Phys. D 35, 2550097 (2026)
- S. Isayama, H. Shimooka, R. Kono, & S. Matsukiyo, J. Geophys. Res. 131, e2025JA034515 (2026)
文献 [7,8,11] は OpenMHD をベースに開発した double-polytropic MHD コードを使っています。コードを使ってみたい方は個別にご連絡ください。
解説記事
教育利用
以下の修士/卒業研究に OpenMHD を利用していただいています。
- 名下宥佑、宇宙プラズマ中の磁気リコネクションに対する三次元磁場成分の影響(神戸大学工学部 2021年卒業論文)
- 渡邉悠太郎、宇宙プラズマ中の磁気リコネクションが生成する衝撃波構造の研究(神戸大学工学部 2022年卒業論文)
- 山本百華、宇宙プラズマ中の密度非対称条件下での磁気リコネクションの MHD シミュレーション(神戸大学大学院工学研究科 2022年修士論文)
- 早瀬理紘、宇宙プラズマ中の磁気リコネクションの内部に生じる渦構造の検討(神戸大学工学部 2023年卒業論文)
- 下岡暉、PINNs による磁気リコネクション構造の再構築(九州大学大学院総合理工学府 2025年修士論文)
- 蓼沼和希、太陽彩層弱電離環境下における磁気リコネクション衝撃波解析(東京大学理学部 2026年卒業論文)
流体力学・MHD シミュレーションの基礎理論
- MHDシミュレーションの基礎 -- 広島大学(当時)の草野先生による解説記事。PDF ファイル。
- 磁気流体力学方程式に対する近似リーマン解法 -- 広島大学の三好先生による HLLD 法の解説記事です。CANS+ コードのドキュメントの一部。
- 近似的リーマン解法 ―流体計算― -- 千葉大学の山下和之先生による Roe 法シミュレーションの解説記事。
- 数値流体力学大全 -- 東北大学の大宮司先生による解説記事。数値計算の基礎から流体シミュレーションについて。
- 物理学特殊講義I・計算物理学特別講義III -- 法政大学の松本先生による天体 HD・MHD・AMR シミュレーションの集中講義の資料です。お勧め!
- 研究紹介:おすすめ書籍 でも参考になりそうな書籍を紹介しています。
MHD コード
- CANSコード -- 京都大学花山天文台の横山先生が開発した Fortran 77 の MHD コード。 Lax--Wendroff 法・Roe 法・CIP 法で、並列手法は MPI です。 私はこのコードでMHDシミュレーションの勉強を始めたのですが、 いま始めるなら C/C++ か modern Fortran のコードを使った方が良いでしょう。
- CANS+ コード -- 千葉大学の松本先生らが開発・公開している MP5 + HLLD 法の MHD コード。 言語は Fortran 90 で、並列手法は MPI + OpenMP のハイブリッド方式です。 日本語ドキュメントが充実しています。 名前は CANS+ ですが、上記の CANS とは全く別のコードです。
- qasMHD コード -- 海洋研究開発機構の簑島さんが開発・公開している MHD コード。 幅広いパラメーターレンジで高精度を保つ low-dissipation HLLD 法を採用しています。 言語は C++ で並列手法は MPI + OpenMP のハイブリッド方式。
- PLUTO コード -- イタリアの Mignone さんらが開発している有限体積型 MHD コード。 C 言語、MPI 並列、相対論 MHD にも対応。英語ドキュメントも充実しています。 外部ライブラリを使って AMR にも対応可能。
- Athena MHD code -- 天文分野で良く使われている有限体積型 MHD コード。C 言語、MPI 並列。
- Athena++ コード -- Athena コードを拡張した一般相対論磁気流体コード。C++ 言語、MPI + OpenMP ハイブリッド並列。
- SFUMATO コード -- 法政大学の松本先生が開発されている AMR 磁気流体コード(非公開)。Fortran 90 言語、MPI 並列。
Fortranと並列プログラミング
- Fortran入門 -- NAG 社による Fortran 90/95 言語のオンラインテキスト。
- Fortran演習 -- 東大地惑・3年生の「地球惑星物理学演習」で使われている Fortran 90 プログラミング入門テキスト。
- Fortranをコーディングする際に気をつけていること -- Fortranでコーディングをする際のヒント。@implicit_none さん。
- 計算科学演習A -- 神戸大学大学院システム情報学研究科の Fortran 90 プログラミング・並列計算の講義資料。
- セミナー資料 公開ページ -- 高度情報科学技術研究機構が開催したHPCプログラミングセミナーの資料。
- RIKEN AICS HPC Summer School 2014 -- 理研・計算科学研究機構が開催した講習会のビデオ・講演資料(PDF)。中・上級者向け。
- 配信講義 計算科学技術特論A (2017) -- 理研・計算科学研究機構が開催した遠隔講義のビデオ・講義資料(PDF)。上級者向け。
- 配信講義 計算科学技術特論A (2019) -- 同じ講義のアップデート版。
- 実践MPI‐2【書籍】 -- Using MPI-2: Advanced Features of the Message-Passing Interface の邦訳版で、並列入出力(MPI-IO)など MPI-2 の進んだ機能を解説しています。開発者にとっては MPI-2 は今も使う技術の基礎ですから、まとまった日本語の解説は重宝します。たまに見かける格安の中古本も狙い目ではないでしょうか。
- MPI version 2.2日本語訳 -- MPI 2.2 の規格書をPCクラスタコンソーシアムが日本語に翻訳したものです。
- 高度情報科学技術研究機構 セミナー資料 -- OpenMP と MPI を使った「並列プログラミング入門」や講義資料とサンプルプログラムがあります。「チューニング技法入門」も参考になります。
- OpenMP入門 -- NAG 社による OpenMP プログラミングのオンラインチュートリアル。
- OpenMP入門 (1) (2) (3) -- 九州大学情報基盤センターによる OpenMP の解説記事。PDF ファイル。基礎事項とループ並列化、仕事単位の並列化、性能解析手法について。
- OpenMP Application Program Interface -- OpenMP 3.0 の規格書を富士通が日本語に翻訳したものです。
- 並列プログラミング入門【書籍】 -- OpenMP(および GPU 並列用の OpenACC)によるノード内並列化手法の入門書。日本語の本の中ではこの本が入手しやすいと思います。
- スパコンプログラミング入門【書籍】 -- 日本語で入手しやすい、MPIによるプロセス間並列プログラミングの入門書。
- インテル(R) 64 アーキテクチャーおよび IA-32 アーキテクチャー最適化リファレンス・マニュアル 参考訳 -- 最適化に関する Intel の技術解説書の和訳(800ページ以上!!)が公開されています。
CUDA Fortran
- CUDA Fortran チュートリアル -- NEC による CUDA Fortran 言語の日本語チュートリアル。PDF ファイル。コードの実例付きで参考になりました。
- PGI CUDA Fortran によるGPUプログラミング -- 筑波大学計算科学研究センターの講習会資料(PDF)。
- Parallel Programming with CUDA Fortran -- NVIDIA社の講習会資料(PDF; 英語)。CUDA Fortranプログラミングのクイックガイドに。
- CUDA Fortran Programming Guide -- NVIDIA 社による CUDA Fortran 言語の公式ガイド(英語)。PDF ファイルもダウンロードできます。困ったときに最後に頼れるのはここです。
- CUDA Fortran入門 -- @implicit_none さんによる CUDA Fortran 言語の入門ガイド。
- PGI コンパイラ技術情報・TIPS -- nvfortran の前身、PGI コンパイラ(PGI fortran)を販売していたソフテック社による技術情報・TIPS 集です。
- 第245回 講習会「MPI+OpenMPで並列化されたFortranプログラムのGPUへの移行手法」 -- 東大情報基盤センターによる講習会。講演資料と動画。
- CUDA Fortran for Scientists and Engineers【書籍】 -- CUDA Fortran プログラミングを解説する数少ない書籍(英語)。ウェブの情報を眺めた後、この本に進むのがまとまった知識を得る近道だと思います。2024年の改訂でずいぶん値上げされました。
- Programming Massively Parallel Processors: A Hands-on Approach, 第3版【書籍】 -- The Nvidia Way でも触れられていた CUDA/GPUコンピューティングの教科書。Appendix C に CUDA Fortran の解説があります。注:第4版では CUDA Fortran の章は無くなってしまいました。
- CUDA C プロフェッショナル プログラミング【書籍】 -- C言語の本ですが、CUDAの動作モデルやマルチストリーム処理などを丁寧に解説していて良かったです。
可視化 - Python 3
- Python チュートリアル -- Python 3.14 の公式チュートリアル(日本語版)。基本文法はここで確認できます。
- SciPy Lecture Notes -- 科学技術計算のための Python 3 + 周辺ライブラリの利用方法を解説。打田旭宏さんによる日本語訳。原文はこちら。
- Matplotlib -- Python の可視化環境、Matplotlib の本家ページ。オンラインドキュメントやサンプルが充実しています。
- プログラミング演習 Python 2023 -- 京都大学・喜多先生らが公開しているプログラミング演習授業の教材。
- Pythonプログラミング入門 -- 東京大学 数理・情報教育研究センターの「Pythonプログラミング入門」のテキスト。
- Python演習 -- 東大地惑・3年生の「地球惑星物理学演習」で使われている Python プログラミングの入門テキスト。
- Python による科学技術計算の概要 -- NumPyや機械学習系パッケージを中心に、科学技術計算分野でのPythonの利用方法を概観しています(PDF)。中級者向け。
- 今日からはじめるPython -- プラズマ・核融合学会誌の特集記事 (PDF)。3.1〜3.3 の科学技術系ライブラリの解説が良いです。
- 科学技術計算のためのPython入門【書籍】 -- Pythonの言語仕様と科学技術系ライブラリをコンパクトに概観していて、Python中級者や(私のような)他言語からPythonに乗り換えたユーザーにお薦めできる本です。2章と3章は飛ばして後で読んでも良いかもしれません。サポートページにアップデート情報も。
- Pythonデータサイエンスハンドブック【書籍】 -- Python のデータ解析ツール(IPython, NumPy, Matplotlibなど)の使い方を解説しています。英語の原著(Python Data Science Handbook)もオンラインで公開されています。
- 早く知っておきたかったmatplotlibの基礎知識、あるいは見た目の調整が捗るArtistの話 -- Matplotlib のオブジェクト構造やグラフの調整方法に関する日本語ノート。
可視化 - IDL
- IDL講習会資料 -- ASIAA 大山さんと国立天文台・天文データセンター巻内さんによるデータ解析講習会資料。IDL の日本語チュートリアルとして、いちばんお勧め。
- IDLメモ -- 京大花山天文台の西田さんによる IDL 覚書き。
- NV5 Geospatial Japan > 技術情報 > 技術資料(日本語) -- IDL の国内販売元による日本語ドキュメント。
- IDL - 地物いろいろ -- 地球物理分野の学生有志が IDL の使い方をまとめたサイト。
- IDLプログラミング入門【書籍】 -- 現代的な IDL の事実上唯一の日本語入門書。基礎文法やオブジェクトグラフィックスを解説しています。