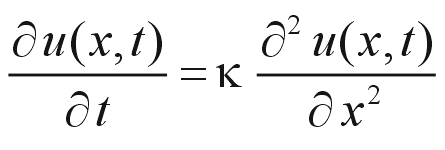
○ 偏微分方程式を解く 〜 拡散方程式を解いてみる 〜
先週まで常微分方程式の解法を取り扱いました。今回は偏微分方程式を扱います。偏微分方程式の数値解法は、計算機シミュレーションの王道です。例えば、流体力学のシミュレーションは、偏微分方程式を数値的に解いているのだと言うことができます。とはいっても基本的な考え方は常微分方程式と同じで、方程式を「差分近似」して離散化して計算します。
一口に偏微分方程式といってもいろいろなものがあるわけですが、物理の問題としては2階や1階のの偏微分方程式がよく出現します。2階の偏微分方程式はその形から、(1)楕円型 (ラプラス方程式)、(2)双曲型(波動方程式)、(3)放物型(拡散方程式)、に分類されます。それぞれに、適当な数値解法が考案されています。今回は、(3)の放物型方程式のもっとも簡単な拡散方程式を解いてみましょう。
・拡散方程式
拡散方程式の形は
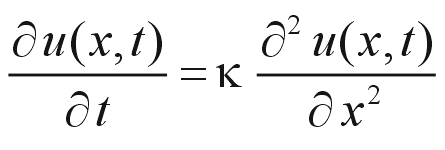
です。実際上の例としては、κを熱伝導係数と見れば熱伝導方程式になります。
・方程式の規格化
数値的に解く場合には、我々が普通に使う単位系(SIとかCGSとか)をそのまま計算することはしません。数値計算として必要な精度を保つためには、通常の単位をそのまま計算するのは必ずしも得策ではないからです。例えば太陽系形成のシミュレーションを行うことを考えると、問題設定としては数10億年程度の時間スケールを計算することになりますが、SI系を使って秒を単位に計算するというのは意味がありません。この場合、1億年を1となるような単位を取れば十分です。時刻を表す物理変数 t を Tという単位(この場合、1億年)で表現し直して、 t/T → τ としてあげるとτは無次元の量になります。方程式中に現れるすべての変数に対して同様に無次元化してあげると、最後には完全に無次元化された方程式になります。このとき、各項の係数の値はできるだけ1にするようにするのがコツです。数値計算上はできるだけシンプルな方程式を解くことによって相対的な誤差を最小にすることができます。このような作業を規格化といいます。拡散方程式も問題に応じて適当に規格化すれば、拡散係数κ=1にすることができます。したがって、ここで解くべき方程式は
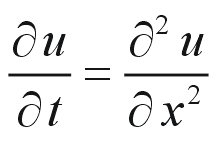
で十分です。
・問題設定
今回は解くべき問題を以下のように定義します。
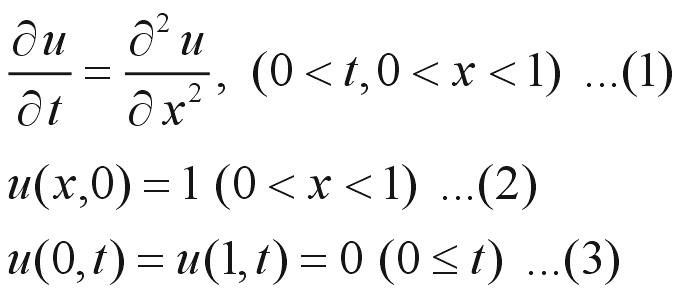
(1)は方程式そのものです。問題設定としては、拡散方程式の u(x,t) に対して u(x,0) が与えられた時の t>0 における u の振る舞いを知りたい、ということになります。(2)でt=0での u の初期条件を設定しています。また、(3)で、u の境界値を定義する必要があります。今回は x=0, x=1 では常に u=0 となるように固定しました。
この問題を熱伝導の問題と考えるならば、u は温度で、厚さ1の物体がある場合の物体の初期温度が一様であったものを、両端の温度を強制的に固定した場合に、物体内部の温度分布が時間とともにどう変わるのかを調べる問題である、といえます。
・方程式の離散化
常微分方程式の場合と同じく、時間、空間の変数 t, x は離散化して、それぞれΔt、Δx ごとに分割します。
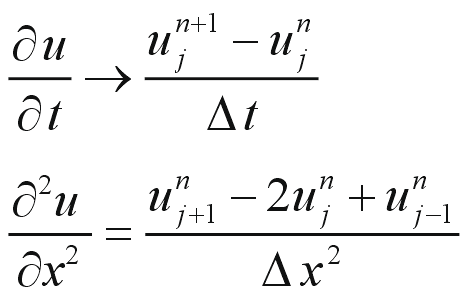
Jmax = 1/Δx とすると、j = 0, 1, 2, ... , Jmax となります。また、n = 0, 1, 2, ... となります。n の上限値は必要な時間分だけ大きくとることになります。
結局、解くべき離散化された拡散方程式は
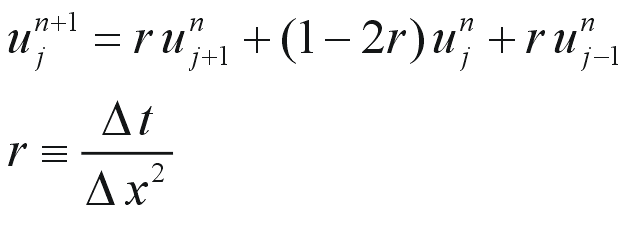
となります。以上をプログラムに書くとリスト1のようになります。
リスト1
1 program main
2 implicit none
3
4 integer,parameter:: jmax=10
5 integer,parameter:: nmax=250
6 integer,parameter:: nint=25
7
8 real,dimension(0:jmax):: u
9 real,dimension(1:jmax-1):: unew
10 real delx,delt,r
11
12 integer j,n
13
14 character(len=10) fname
15
16 delx=1.0/real(jmax)
17 delt=0.004
18 r=delt/delx**2
19
20 u(0)=0.0
21 do j=1,jmax-1
22 u(j)=1.0
23 end do
24 u(jmax)=0.0
25
26 do n=0,nmax
27
28 if (mod(n,nint)==0) then
29 write(fname,'(a,i5.5,a)') 't',n,'.dat'
30 open(10,file=fname)
31 do j=0,jmax
32 write(10,'(2f12.5)') real(j)*delx,u(j)
33 end do
34 close(10)
35 end if
36
37 do j=1,jmax-1
38 unew(j)=u(j+1)*r+u(j)*(1.0-r*2.0)+u(j-1)*r
39 end do
40
41 do j=1,jmax-1
42 u(j)=unew(j)
43 end do
44
45 end do
46
47 end program
リスト1の場合は、時間方向の微分の精度はΔtの1次精度、空間方向にはΔxの2次精度の計算になります。今回の計算の場合は、次の時間ステップの量 u(n+1) を求めるための右辺の量にすべて既知の量を使えたので非常にシンプルな解法になりました。このように、u(n+1) を既知の量のみから求めることができる解法を「陽的解法」と呼びます。
実は、拡散方程式の場合、上記の離散化を行うと時間方向の積分を安定に行う為には
r < 1/2
である必要があることが知られています。(安定性条件)
この為、空間を精度よく解こうと思って、Δx を小さくすると、時間刻み幅Δt を非常に小さくとらなくならなければならないので、非常に計算量が多くなるという欠点があります。
・クランクーニコルソン法
これまでの例では、安定性に問題がありました。これを改善するために少し差分近似の方法を変更してみましょう。
時間方向の精度が1次だったので2次に変えることを考えてみます。
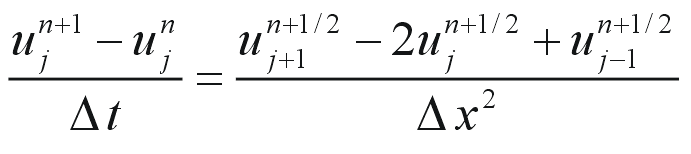
とすれば、時間についても2次の精度にすることができます。しかし、n+1/2の u が必要となってしまいます。これを、n と n+1 の時の u の平均と思って
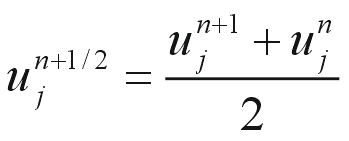
と表現することにしましょう。すると、離散化された拡散方程式は
![]()
となります。今回は u(n+1) に対して、単純に u(n) のみで書き下すことができずに、u(n+1)の情報がなければ u(n+1) を解くことができません。このような場合を陽的解法に対応して「陰的解法」と呼びます。
上記の方程式を解く場合には
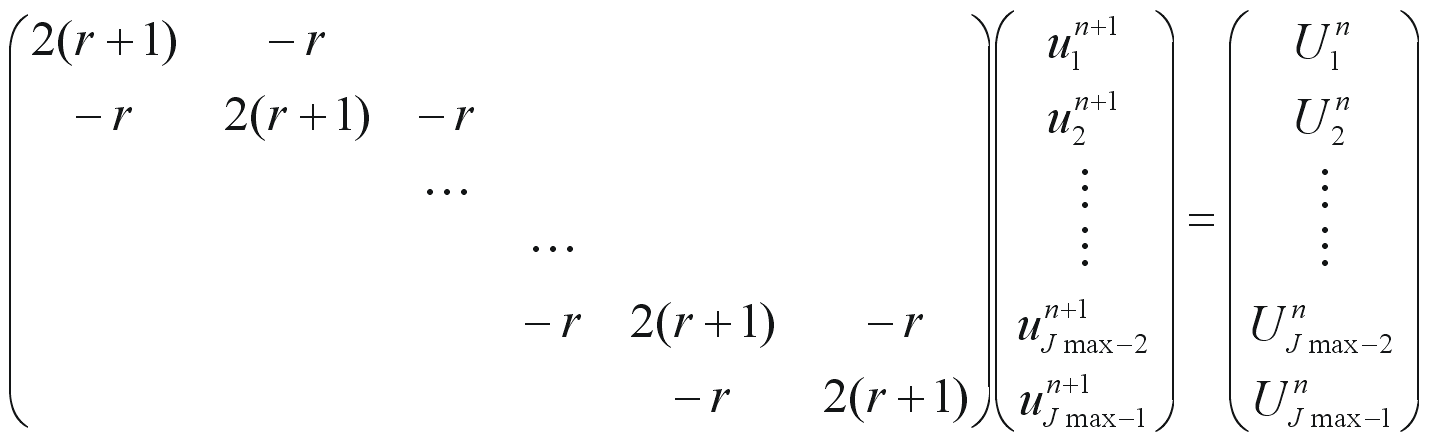
のような3重対角の連立1次方程式を解く必要があります。(U(n)とは右辺の値(既知の量から計算できる量)です。)
陰的解法のメリットは、Δt の刻み幅を大きくしても時間方向の積分が安定に行えるというメリットがあります。(無条件安定) ただし、Δt を大きくとった場合、必ずしも真の階に近い値が計算できている保証がないので、問題に応じて陽的解法と陰的解法は使い分ける必要があります。
以上の解法をクランクーニコルソン法と呼びます。クランクーニコルソン法を使ったプログラムをリスト2に示します。リスト2中に現れる tridag というサブルーチンは3重対角行列で表される連立1次方程式を解くためのものです。a,b,cに3重対角項のそれぞれの値をいれて、dに右辺の値をいれて、サブルーチンに渡してやるとxに階が戻ってきます。最後のnは行列の次元数です。今回はJmax-1になります。wは作業用の変数なので特に値を設定する必要はありません。
リスト2
1 program main
2 implicit none
3
4 integer,parameter:: jmax=10
5 integer,parameter:: nmax=250
6 integer,parameter:: nint=25
7
8 real,dimension(0:jmax):: u
9 real,dimension(jmax-1):: a,b,c,d,x,w
10
11 real delx,delt,r
12
13 integer j,n
14
15 character(len=10) fname
16
17 delx=1.0/real(jmax)
18 delt=0.004
19 r=delt/delx**2
20
21 u(0)=0.0
22 do j=1,jmax-1
23 u(j)=1.0
24 end do
25 u(jmax)=0.0
26
27 do n=0,nmax
28
29 if (mod(n,nint)==0) then
30 write(fname,'(a,i5.5,a)') 't',n,'.dat'
31 open(10,file=fname)
32 do j=0,jmax
33 write(10,'(2f12.5)') real(j)*delx,u(j)
34 end do
35 close(10)
36 end if
37
38 do j=1,jmax-1
39 a(j)=-r
40 b(j)=(r+1.0)*2.0
41 c(j)=-r
42 end do
43 d(1)=u(2)*r-u(1)*(r-1.0)*2.0+u(0)*r*2.0
44 do j=2,jmax-2
45 d(j)=u(j+1)*r-u(j)*(r-1.0)*2.0+u(j-1)*r
46 end do
47 d(jmax-1)=u(jmax)*r*2.0-u(jmax-1)*(r-1.0)*2.0+u(jmax-2)*r
48
49 call tridag(a,b,c,d,x,w,jmax-1)
50 do j=1,jmax-1
51 u(j)=x(j)
52 end do
53
54 end do
55
56 end program
57
58 subroutine tridag(a,b,c,d,x,w,n)
59 implicit none
60
61 integer n
62 real,dimension(n):: a,b,c,d,x,w
63
64 real bet
65 integer j
66
67 bet=b(1)
68 x(1)=d(1)/bet
69 do j=2,n
70 w(j)=c(j-1)/bet
71 bet=b(j)-a(j)*w(j)
72 x(j)=(d(j)-a(j)*x(j-1))/bet
73 end do
74 do j=n-1,1,-1
75 x(j)=x(j)-w(j+1)*x(j+1)
76 end do
77
78 return
79 end subroutine tridag
・課題
陽的解法と陰的解法のそれぞれの場合について、いくつかのΔt, Δxの組に対して解の振る舞いを比較してみてください。