○　常微分方程式を解く

〜　微分方程式の初期値問題の数値解法について　〜

　先週までは数値微分の方法について学びました。次は微分方程式を数値的に解くことを考えてみましょう。数学の時間には微分方程式の解法についていろいろと勉強したと思います。しかし、解析的な解が得られる場合であっても特殊関数等がでてきて、解の振る舞いが直ぐには思い浮かびません。また、解析的な解が得られない場合も多く、「ある特定の場合についての結果を知りたい」には数値解法が大変役に立ちます。

　ここではまず常微分方程式の初期値問題についての解き方を説明します。例えば、人工衛星の軌道計算などのように、「ある時間での位置と速度が正確に求まっている場合、その物体が将来どのような運動をするのか」を予測するような問題があります。

初期値問題をもう少し数学的に定義すると

微分方程式　

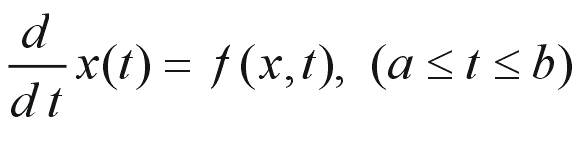
に対して、初期条件

を与えて

を求める問題ということになります。

ここで、1階の微分方程式の表示をしましたが、一般的にN階の高階微分方程式はN元の連立1階微分方程式に帰着できますから、1階の微分方程式の解法を調べれば十分ということになります。

・ Euler法

さて、数値微分の時にもっとも簡単な微分の差分近似として、

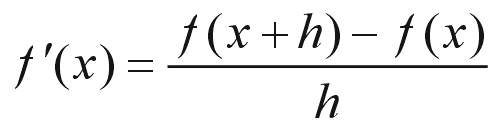
がありました。この表式を応用して微分方程式を差分方程式化してみましょう。

つまり、刻み幅 "h" を定めて、独立変数 t の値における x の近似値を

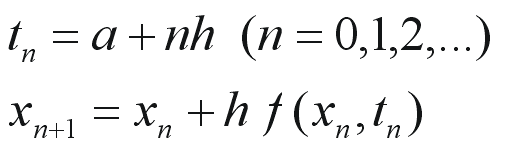
として、順々に近似値を求めていけばよさそうです。

この方法を Euler 法と呼びます。数値微分の時と同じく、刻み幅 h を粗くとれば取るほど近似精度が悪くなることが予想できますが、まずは、例題をときながらこの点を確認してみましょう。

例題として、

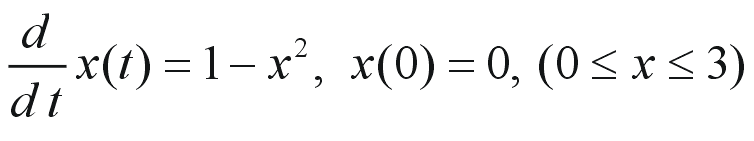
を解いてみましょう。この微分方程式の解析解は

です。

Euler 法でこれを解くプログラムを以下に示します。

 
program main
  implicit none
 
  real tstart,xstart,tend,h 
  real t,x,f
 
  character(len=12) fname  ! 文字の宣言（12文字まで）
 
  write(*,'(a,$)') 'tstart, x(tstart) ? '
  read(*,*) tstart,xstart
 
  write(*,'(a,$)') 'tend, dt ? '
  read(*,*) tend,h
 
  write(*,'(a,$)') 'file name ? '
  read(*,*) fname
 
  open(10,file=fname)
 
  t=tstart
  x=xstart
  do while (t<=tend)
    f=tanh(t)   ! 解析的な解
    write(10,'(3f13.5)') t,x,abs(x-f)
    x=x+(1.0-x**2)*h  ! xn+1=(1-xn2)*dt+xn
    t=t+h
  end do
 
  close(10)
 
end program main

結果を図に示します。 h が大きいほど真の値からの誤差が大きいことがわかります。

今回の場合、x(t) が 1 に漸近するので、ステップが進んでも誤差が蓄積しませんでしたが、一般的には n が大きくなって t が初期値より離れれば離れるほど誤差が貯まって真の値から離れてしまいます。

さて、Euler 法の問題は、精度よく微分方程式の解を求めようと思うと、小さな h を選ばなければならないことです。微分方程式の右辺 f の形が、例の場合は単純でしたが、もっともっと複雑になったり、初期値問題の定義される範囲がずっと広かったり（つまり (b-a)/h がとても大きい。）、すると計算時間が非常に長くなってしまう可能性があります。また、誤差が蓄積した結果、数値解が発散してしまうなどの「不安定」を示すこともあります。

　より高精度の計算結果を得る方法としては、次に紹介する Runge-Kutta 法が有名です。

・ Runge-Kutta法

Euler法は

を元にしているので、n を進める毎に O(h2) の誤差が累積することになります。

そこで、近似の考え方を少し進めてみましょう。まず、1つのステップの間 (tn < t < tn+1)の中点まで「仮に」近似を進めます。そして、その中点での値から微分方程式の右辺の値を計算して、Euler 法に修正を加えようというアイディアになります。

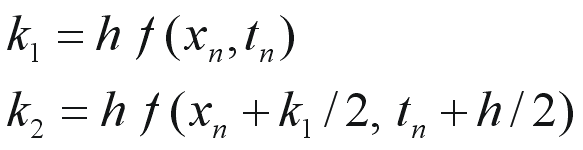
という、2つの右辺の近似値の内、k2 を採用すると

となり、近似精度があがります。このように区間の中途点での近似値をいくつか計算し、その組み合わせでより精度の高い近似公式を求めることが可能になります。

　よく知られたものは4次のRunge-Kutta法です。4次のRunge-Kutta法の表式は次のようになります。

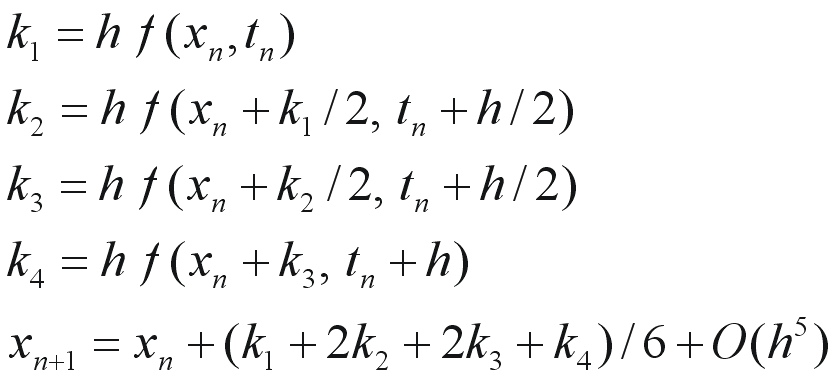
4次のRunge-Kutta法を用いて、先程の例と同じ微分方程式を解くためのプログラムを以下に示します。

program main
  implicit none
 
  real tstart,xstart,tend,h
  real t,x,f
  real k0,k1,k2,k3
  real f0,f1,f2,f3
 
  character(len=12) fname
 
  write(*,'(a,$)') 'tstart, x(tstart) ? '
  read(*,*) tstart,xstart
 
  write(*,'(a,$)') 'tend, dt ? '
  read(*,*) tend,h
 
  write(*,'(a,$)') 'file name ? '
  read(*,*) fname
 
  open(10,file=fname)
 
  t=tstart
  x=xstart
  do while (t<=tend)
    f=tanh(t)
    write(10,'(2f13.5,e13.5)') t,x,abs(x-f)
    k0=x              ! k0:xn
    f0=(1.0-k0**2)    
    k1=x+f0*h/2.0     ! k1:xn+k0/2
    f1=(1.0-k1**2)
    k2=x+f1*h/2.0     ! k2:xn+k1/2
    f2=(1.0-k2**2)
    k3=x+f2*h         ! k3:xn+k2
    f3=(1.0-k3**2)
    x=x+(f0+f1*2.0+f2*2.0+f3)*h/6.0
    t=t+h
  end do
 
  close(10)
 
end program main

例えば、同じ刻み幅 h=0.1 を取った場合の近似精度がどれ程ことなるかを確認してみて下さい。h が大きくても Euler法よりも遙かによい近似を得ることが確認できましたか？

　さて、上のプログラムリストでは、微分方程式が変わるたびに右辺の定義部分を何カ所も変更しなくてはならなくって不便です。これを Fortran の function という機能を使って変更してみましょう。

program main
  implicit none
 
  real tstart,xstart,tend,h
  real t,x
  real t0,t1,t2,t3
  real k0,k1,k2,k3
  real f0,f1,f2,f3
 
  real func
 
  character(len=12) fname
 
  write(*,'(a,$)') 'tstart, x(tstart) ? '
  read(*,*) tstart,xstart
 
  write(*,'(a,$)') 'tend, dt ? '
  read(*,*) tend,h
 
  write(*,'(a,$)') 'file name ? '
  read(*,*) fname
 
  open(10,file=fname)
 
  t=tstart
  x=xstart
  do while (t<=tend)
    write(10,'(2f13.5)') t,x
 
    t0=t
    k0=x
    f0=func(t0,k0)
 
    t1=t+h/2.0
    k1=x+f0*h/2.0
    f1=func(t1,k1)
 
    t2=t+h/2.0
    k2=x+f1*h/2.0
    f2=func(t2,k2)
 
    t3=t+h
    k3=x+f2*h
    f3=func(t3,k3)
 
    x=x+(f0+f1*2.0+f2*2.0+f3)*h/6.0
 
    t=t+h
  end do
 
  close(10)
 
end program main
 
real function func(t,x)
  implicit none
 
  real t,x
 
  func=(1.0-x**2)
 
  return
end function func

詳しい文法の説明は文法テキストの "8.2.1. 関数副プログラム"という項目を見て下さい。この書き換えによって微分方程式が変わっても、右辺の定義を func の中で変更すればよいだけとなってすっきりとします。

【アドバンス】 Runge-Kutta法の刻み幅制御

　私たちが微分方程式を解きたい時は、その解の性質がよくわからないことが多い。そのため、刻み幅 h をどの程度の大きさにとれば十分か判断に困ることがあります。例えば、関数 x(t) が h に対してゆっくりとしか変化しない場合は h の値を大きくして計算反復回数を減らしてあげたいし、逆に、h の間に x(t) が急激に変化する場所では必要精度を確保するために h の値を小さくしてあげる必要があります。h の値を自由に変えて必要精度を確保できるようになると微分方程式の初期値解法としてはかなり万能になります。

　実際、そのような刻み幅を自動制御する Runge-Kutta 法が開発されています。自動制御の原理についてはここでは説明をしませんが、次に挙げる参考書などに考え方とプログラムが載っていますので、興味がある方は勉強してみて下さい。

・ニューメリカルレシピ・イン・シー「日本語版」　丹慶勝市他訳　技術評論社　（１９９３）
・FORTRAN77 数値計算プログラミング　森　正武　岩波書店（１９８６）

この授業では「FORTRAN77 数値計算プログラミング」に掲載されていた刻み幅自動制御のRunge-Kutta法プログラムを FORTRAN90 へ書き直したものを使用します。　このプログラムを利用するためには、「サブルーチン」という機能を使います。サブルーチンの文法的な説明については文法テキストの "8.1 サブルーチン" という章を見て下さい。


サンプルプログラムについてはこちらを見て下さい。


・次回(第七回)の課題