Numerical simulation of the deep weak lensing survey with the Hubble volume simulation data

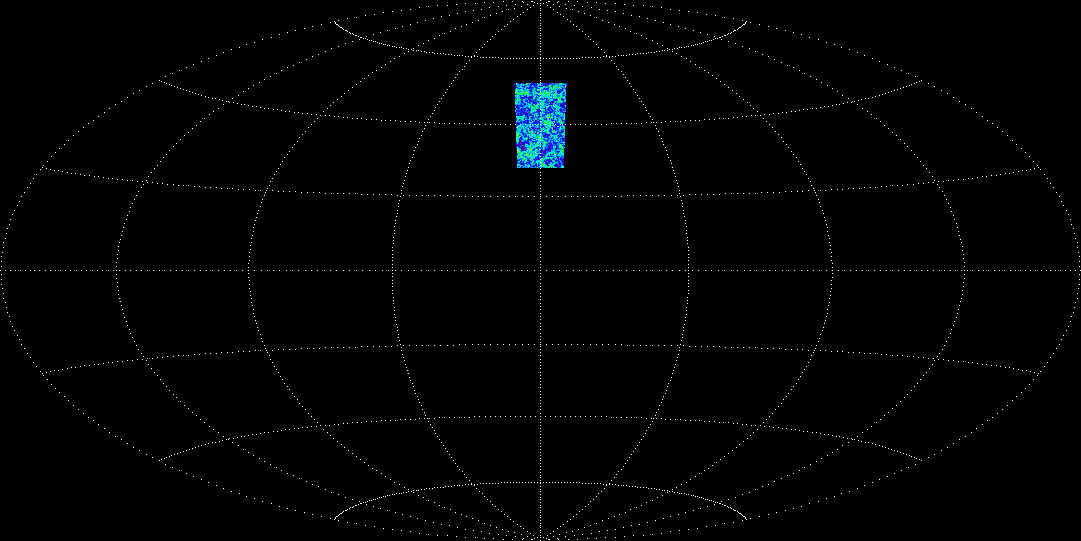
Figure 1

Figure 1 shows the lensing convergence map of the DEEP WEAK LENSING SURVEY region (13.65x27.3 sq. degrees).
The lensing convergence was obtained from the ray-tracing simulation combined with the Hubble volume simulation data, the largest N-body simulation in the world.
The "wedge" data set of the Hubble volume simulation was used (see Hubble simulation web site for more details of the Hubble volume simulation).

Since the Hubble volume simulation data does not reach to the last scattering surface (z=1100), we used the Hubble simulation data for redshift range between z=0 and z=4.38, at redshift higher than that, uniform mass distribution is assumed.

Figure 2

Figure 2 is the zoom-in map of Figure 1 and shows the convergence map of source redshift of 3 (the last scattering surface). Click here to find same maps but for redshift 1 and 1100 (the last scattering surface)

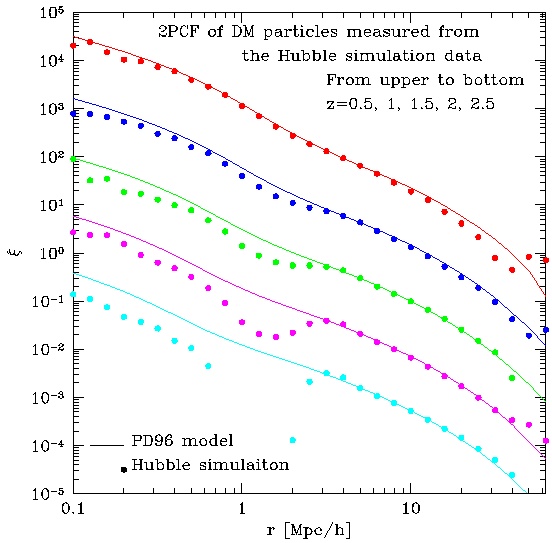
Figure 3 (Note, the amplitudes are shifted vertically by +2, +1, 0, -1, -2 [in log scale] for z=0.5, 1.0, 1.5, 2.0 and 2.5, respectively, for clarify.)

Figure 3 shows the two-point correlation functions of the dark matter particles in the Hubble volume simulation (filled circles) compared with the nonlinear predictions (solid lines).
This Figure indicates a weak point of the higher resolution simulation such like P3M simulation, that is, at an early stage of the structure formation, correlations (or powers in Fourier space) at small scales are not reliably reproduced, but small scale powers are systematically underestimated. This has an impact on the weak lensing simulations, especially for a higher source redshift cases (shown in Figures 4, 5 and 6).

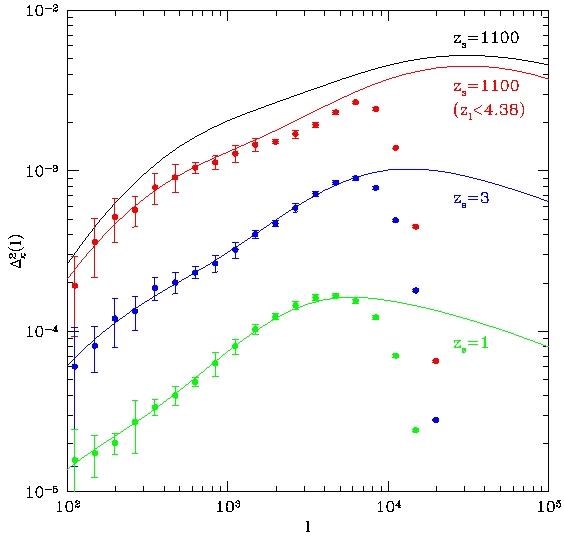
Figure 4

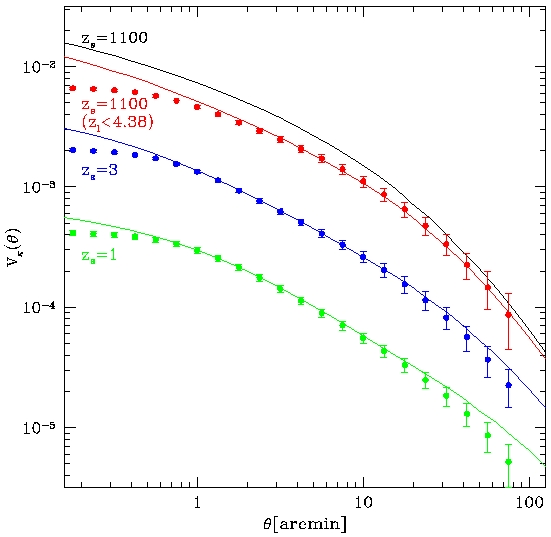
Figure 5

Figure 4 shows the power spectrum of the lensing convergence, and Figure 5 shows the variance of the lensing convergence smoothed by the 2-dimensional Top-Hat filter as a function of the smoothing scale.
Very good agreements between measurements and predictions down to 0.8 arcmin are found.
The dumping of the amplitude at scale smaller than 2 arcmin for z=1100 case is due to the lack of the small scale power in the matter distribution at redshift higher than 2 shown in Figure 3.

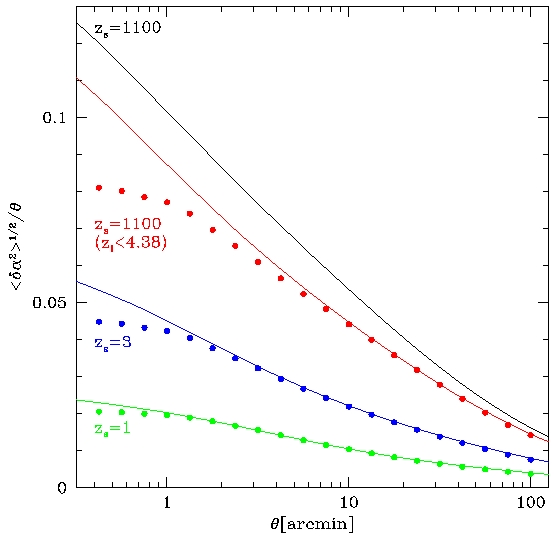
Figure 6

Figure 6 shows the root-mean-square of the lensing excursion angles between nearby light rays compared with the nonlinear prediction. Again very good agreements between measurements and predictions are found.

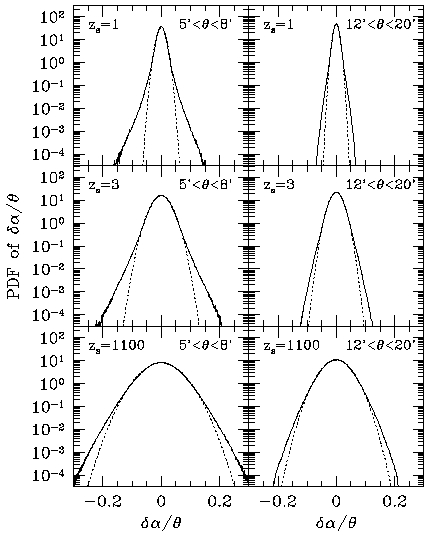
Figure 7

Figure 7 shows the probability distribution function of the difference in the deflection angles between nearby two light rays (so-called lensing excursion angle) normalized by their intrinsic separation (the solid curves). The dotted curves show Gaussian distribution with the sigma computed from the measured PDFs.
The deviation from the Gaussian distribution is evident, the exponential tail is clearly shown. See Hamana & Mellier (2001) for discussion about effects of the non-Gaussian nature in the PDF on the weak lensing of the cosmic microwave background.

Buck to the top page

Takashi Hamana
Last update: 01/03/2001